题目内容
若A,B均在抛物线y2=-8x上,点O为坐标原点,且OA⊥OB,则直线AB一定会经过点________.
(-8,0)
分析:设出AB的方程,A,B的坐标,进而把直线与抛物线方程联立消去y,根据韦达定理求得x1+x2和x1x2的表达式,进而利用抛物线方程求得y1y2=的表达式,进而根据AO⊥BO推断出x1x2+y1y2=0,求得b与k的关系,即可求出结果.
解答:显然直线AB的斜率存在,记为k,AB的方程记为:y=kx+b,(b≠0),A(x1,y1),B(x2,y2),将直线方程代入y2=-8x得:k2x2+(2kb+8)x+b2=0,则有:
x1+x2=- ,x1x2=
,x1x2=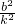 ,又y12=-8x1,y22=-8x2
,又y12=-8x1,y22=-8x2
∴y1y2= ;
;
∵AO⊥BO,∴x1x2+y1y2=0,
得:b=8k
∴直线AB的方程为y=kx+8k,
∴直线AB过定点(-8,0)
故答案为:(-8,0).
点评:本题主要考查了抛物线的简单性质,涉及到直线与圆锥线的问题一般是联立方程,设而不求,属于中档题.
分析:设出AB的方程,A,B的坐标,进而把直线与抛物线方程联立消去y,根据韦达定理求得x1+x2和x1x2的表达式,进而利用抛物线方程求得y1y2=的表达式,进而根据AO⊥BO推断出x1x2+y1y2=0,求得b与k的关系,即可求出结果.
解答:显然直线AB的斜率存在,记为k,AB的方程记为:y=kx+b,(b≠0),A(x1,y1),B(x2,y2),将直线方程代入y2=-8x得:k2x2+(2kb+8)x+b2=0,则有:
x1+x2=-
 ,x1x2=
,x1x2=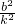 ,又y12=-8x1,y22=-8x2
,又y12=-8x1,y22=-8x2∴y1y2=
 ;
;∵AO⊥BO,∴x1x2+y1y2=0,
得:b=8k
∴直线AB的方程为y=kx+8k,
∴直线AB过定点(-8,0)
故答案为:(-8,0).
点评:本题主要考查了抛物线的简单性质,涉及到直线与圆锥线的问题一般是联立方程,设而不求,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
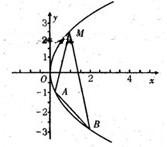 过抛物线C:y2=2px(p>0)上一点
过抛物线C:y2=2px(p>0)上一点 作倾斜角互补的两条直线,分别与抛物线交于A、B两点.
作倾斜角互补的两条直线,分别与抛物线交于A、B两点.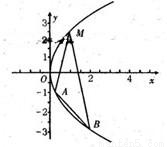
 作倾斜角互补的两条直线,分别与抛物线交于A、B两点.
作倾斜角互补的两条直线,分别与抛物线交于A、B两点.