题目内容
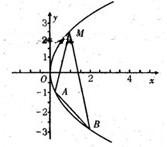
过抛物线C：y2=2px（p＞0）上一点
作倾斜角互补的两条直线，分别与抛物线交于A、B两点．（1）求证：直线AB的斜率为定值；
（2）已知A、B两点均在抛物线C：y2=2px（y≤0）上，若△MAB的面积的最大值为6，求抛物线的方程．
【答案】分析：（1）不妨设
，由KAM=-kBM可得y1+y2=-2p．利用斜率公式可求
（2）AB的方程为：
，即x+y
，由点M到AB的距离d=
及
=
=
，令p+y1=t，可表示
=
，设f（t）=|4p2t-t3|，由偶函数的性质，只需考虑t∈[0，p]，利用导数的知识可得，f（t）在[0，p]单调递增可求三角形的面积的最大值，进而可求p及抛物线的方程
解答：证明：不妨设
由KAM=-kBM可得y1+y2=-2p
∴
（2）AB的方程为：
，即x+y
点M到AB的距离d=
=
=
又由y1+y2=-2p，y1y2＜0y1∈[-2p，0]
令p+y1=t∴t∈[-p，p]
=
设f（t）=|4p2t-t3|为偶函数，故只需考虑t∈[0，p]
f（t）=4p2t-t3，f′（t）=4p2-3t2＞0，f（t）在[0，p]单调递增
当t=p时，f（t）的最小值为：3p3
∴p=2，抛物线方程为：y2=4x
点评：本题主要考查了直线与抛物线的位置关系的应用，要求考试具备一定的计算与推理的能力，试题具有一定的综合性．
，由KAM=-kBM可得y1+y2=-2p．利用斜率公式可求（2）AB的方程为：
，即x+y，由点M到AB的距离d=及==，令p+y1=t，可表示=，设f（t）=|4p2t-t3|，由偶函数的性质，只需考虑t∈[0，p]，利用导数的知识可得，f（t）在[0，p]单调递增可求三角形的面积的最大值，进而可求p及抛物线的方程解答：证明：不妨设
由KAM=-kBM可得y1+y2=-2p
∴
（2）AB的方程为：
，即x+y点M到AB的距离d=
==又由y1+y2=-2p，y1y2＜0y1∈[-2p，0]
令p+y1=t∴t∈[-p，p]
=设f（t）=|4p2t-t3|为偶函数，故只需考虑t∈[0，p]
f（t）=4p2t-t3，f′（t）=4p2-3t2＞0，f（t）在[0，p]单调递增
当t=p时，f（t）的最小值为：3p3
∴p=2，抛物线方程为：y2=4x
点评：本题主要考查了直线与抛物线的位置关系的应用，要求考试具备一定的计算与推理的能力，试题具有一定的综合性．
练习册系列答案
相关题目
过抛物线C：y2=2px（p＞0）上一点
设直线过抛物线C：y2=2px（p＞0）的焦点F，且交C于点M，N，设
（2013•浙江二模）如图，过抛物线C：y2=4x上一点P（1，-2）作倾斜角互补的两条直线，分别与抛物线交于点A（x1，y1），B（x2，y2）