Question

（2013•太原一模）在三棱锥P-ABC中，△ABC是边长为2的正三角形，PA=PB=PC．且PA，PB，PC两两互相垂直，则三棱锥P-ABC外接球的表面积为

6π

．

Answer 1

分析：以PA、PB、PC为过同一顶点的三条棱，作长方体如图，则长方体的外接球同时也是三棱锥P-ABC外接球．算出长方体的对角线即为球直径，结合球的表面积公式，可算出三棱锥P-ABC外接球的表面积．

解答：解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图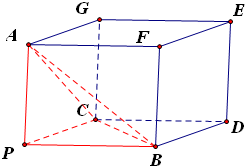
则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为

PA2+PB2+PC2

=

1 2 (22+22+22)

=

6

，
∴球直径为

6

，半径R=

6

2

，
因此，三棱锥P-ABC外接球的表面积是4πR²=4π×（

6

2

）²=6π
故答案为：6π．

点评：本题给出三棱锥的三条侧棱两两垂直，求它的外接球的表面积，着重考查了长方体对角线公式和球的表面积计算等知识，属于基础题．