题目内容
已知抛物线C:y=
x2的焦点为F,直线y=2x-1与C交于A、B两点,则cos∠AFB=( )
| 1 |
| 4 |
分析:确定抛物线C的焦点F,求出点A,B的坐标,利用求向量夹角余弦值的方法,即可得到答案.
解答:解:抛物线C:y=
x2的焦点为F(0,1)
直线y=2x-1代入y=
x2,消去y可得x2-8x+4=0,
∴x1=4+2
,x2=4-2
∴y1=7+4
,x2=7-4
即A(4+2
,7+4
),B(4-2
,7-4
),
∴
=(4+2
,6+4
),
=(4-2
,6-4
),
∴cos∠AFB=
=
=-
故选D.
| 1 |
| 4 |
直线y=2x-1代入y=
| 1 |
| 4 |
∴x1=4+2
| 3 |
| 3 |
∴y1=7+4
| 3 |
| 3 |
即A(4+2
| 3 |
| 3 |
| 3 |
| 3 |
∴
| FA |
| 3 |
| 3 |
| FB |
| 3 |
| 3 |
∴cos∠AFB=
| ||||
|
|
| 16-12+36-48 | ||||||||
|
| 1 |
| 2 |
故选D.
点评:本题考查的知识点是直线与圆锥曲线的关系,其中构造向量然后利用向量法处理是解答本题的重要技巧.

练习册系列答案
相关题目
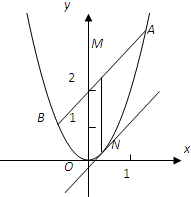 已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.