Question

【题目】正整数数列满足：，．试求通项公式．

Answer 1

【答案】

【解析】

据条件知，数列严格递增．于是，

先在条件式中取，得到，

即． ①

据式①左端得．

则． ②

又由式①右端得，且，

故． ③

据式②、③得整数．

再对条件式中取，得到，

即． ④

由式④左端得．

则．

由式④右端得，即．

因，所以，．故．

继而在已知式中取，得，

即． ⑤

又为正整数，故式⑤右端恒成立．

而由式⑤左端有，故，得．

由，，，，猜想． ⑥

首先，若将式⑥代入已知式得，

即，或．

此式显然成立．

下证：是满足条件的唯一数列．

对归纳．当时已验证．若式⑥对于成立，则对于，据已知式有

． ⑦

由式⑦右端得．

则． ⑧

（这里用到，当时， ．）

据式⑦左端得，

即． ⑨

其判别式

．

设与式⑨对应的关于的一元二次方程的两根为、．

则

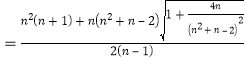
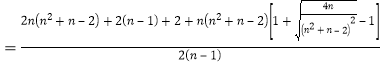
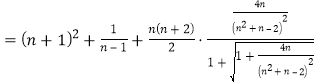
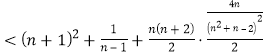
． ⑩

（这里用到，当时， ．）

据式⑧、⑩得．

故由归纳法知，对任意的，式⑥成立，即．