题目内容
已知函数 (a>0),有下列四个命题:
(a>0),有下列四个命题:①f(x)的值域是(-∞,0)∪(0,+∞);
②f(x)是奇函数;
③f(x)在(-∞,0)∪(0,+∞)上单调递增;
④方程|f(x)|=a总有四个不同的解,其中正确的是( )
A.仅②④
B.仅②③
C.仅①②
D.仅③④
【答案】分析:①当a=x=1时f(x)=0,采用举反例的方法得到答案是否正确;
②利用f(-x)+f(x)看是否为0即可判断函数是否为奇函数;
③求出f′(x)判断其符号即可知道函数单调与否;
④|f(x)|=a得到f(x)=±a即x- =±a化简求出x即可判断.
=±a化简求出x即可判断.
解答:解:①当a=x=1时f(x)=0,所以f(x)的值域是(-∞,0)∪(0,+∞),错误;
②f(-x)=-x+ ,而f(x)=x-
,而f(x)=x- ,所以f(-x)+f(x)=-x+
,所以f(-x)+f(x)=-x+ +x-
+x-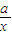 =0得到函数为奇函数,正确;
=0得到函数为奇函数,正确;
③因为f′(x)=1+ ,由a>0得到f′(x)>1>0,所以函数单调递增,正确;
,由a>0得到f′(x)>1>0,所以函数单调递增,正确;
④|f(x)|=a得到f(x)=±a即x- =±a,当a=4时,方程有三个解,错误.
=±a,当a=4时,方程有三个解,错误.
故选B
点评:考查学生会用反例法说明一个命题错误的能力,判断函数单调性及证明的能力,判断函数奇偶性的能力,会判断根的存在性及根的个数的能力.
②利用f(-x)+f(x)看是否为0即可判断函数是否为奇函数;
③求出f′(x)判断其符号即可知道函数单调与否;
④|f(x)|=a得到f(x)=±a即x-
 =±a化简求出x即可判断.
=±a化简求出x即可判断.解答:解:①当a=x=1时f(x)=0,所以f(x)的值域是(-∞,0)∪(0,+∞),错误;
②f(-x)=-x+
 ,而f(x)=x-
,而f(x)=x- ,所以f(-x)+f(x)=-x+
,所以f(-x)+f(x)=-x+ +x-
+x-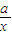 =0得到函数为奇函数,正确;
=0得到函数为奇函数,正确;③因为f′(x)=1+
 ,由a>0得到f′(x)>1>0,所以函数单调递增,正确;
,由a>0得到f′(x)>1>0,所以函数单调递增,正确;④|f(x)|=a得到f(x)=±a即x-
 =±a,当a=4时,方程有三个解,错误.
=±a,当a=4时,方程有三个解,错误.故选B
点评:考查学生会用反例法说明一个命题错误的能力,判断函数单调性及证明的能力,判断函数奇偶性的能力,会判断根的存在性及根的个数的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, (a>0),若
(a>0),若 ,
, ,使得f(x1)= g(x2),则实数a的取值范围是( )
,使得f(x1)= g(x2),则实数a的取值范围是( ) (B)
(B)
 (C)
(C)
 (D)
(D)

 (a>0,且a≠1)
(a>0,且a≠1) (A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且
(A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且 ,则函数y=f(x)在
,则函数y=f(x)在 上的最小值是( )
上的最小值是( )


 其中a>0,e为自然对数的底数。
其中a>0,e为自然对数的底数。
 的单调区间;
的单调区间;