题目内容
若
、b、c均为实数，且＝x2－2y＋
，b＝y2－2z＋
，c＝z2－2x＋
，求证：、b、c中至少有一个大于0.
【证明】 假设、b、c都不大于0，即≤0，b≤0，c≤0，则有＋b＋c≤0.
而＋b＋c＝(x2－2y＋)＋(y2－2z＋)＋(z2－2x＋)＝(x2－2x)＋(y2－2y)＋(z2－2z)＋π＝(x－1)2＋(y－1)2＋(z－1)2＋(π－3)>0，
这与＋b＋c≤0矛盾．
故假设不成立，从而原命题正确．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
（n≥２），其余每个数是它下一行左右相邻两个数的和，如：
＝
Ｂ、
Ｃ、
Ｄ、
，x＝
B．1 C.
D.
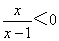},B={x|0＜x＜3},那么“m
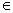A”是“m
的通项公式为
其前
项和为
，则在数列
中，有理项的项数为（ ）
}，B＝{y|y＝2x，x>1}，则A∩B为( )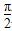
)，sinx＝
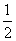，则綈p为( )