题目内容
在△ABC中,已知∠ABC=45°,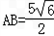 ,D是BC边上的一点,AD=5,DC=3,求AC的长.
,D是BC边上的一点,AD=5,DC=3,求AC的长.
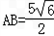 ,D是BC边上的一点,AD=5,DC=3,求AC的长.
,D是BC边上的一点,AD=5,DC=3,求AC的长.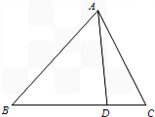
解:在△ABD中,由正弦定理得,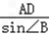 =
=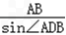
∴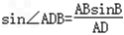 =
= 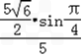 =
=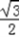
又∵∠ADB∈(0,π),
∴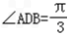 或
或 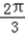 ,
,
①若 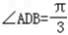 ,则
,则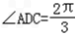 ,
,
在△ADC中,由余弦定理得AC2=AD2+DC2﹣2AD?DCcos∠ADC=49
∴AC=7,
②若 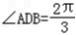 ,则
,则 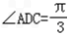 ,
,
在△ADC中,由余弦定理得AC2=AD2+DC2﹣2AD?DCcos∠ADC=19,
∴ 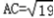 综上所述,AC长为7或
综上所述,AC长为7或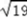

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目