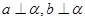题目内容
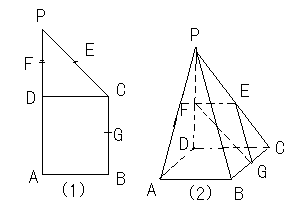
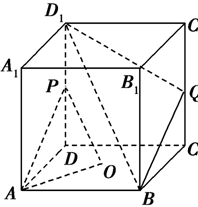
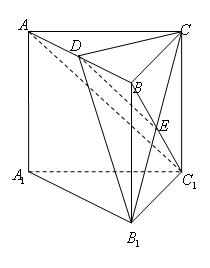
(14分)如图,在直三棱柱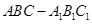 中,
中,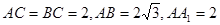 ,点
,点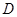 是
是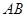 的中点.
的中点.
(Ⅰ)求证: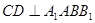 ;
;
(Ⅱ)求证: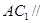 平面
平面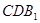 ;
;
(Ⅲ)求异面直线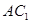 与
与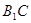 所成角的余弦值.
所成角的余弦值.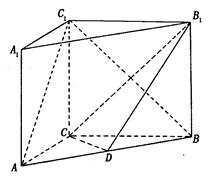
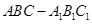 中,
中,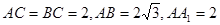 ,点
,点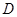 是
是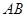 的中点.
的中点.(Ⅰ)求证:
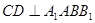 ;
;(Ⅱ)求证:
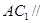 平面
平面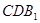 ;
;(Ⅲ)求异面直线
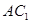 与
与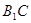 所成角的余弦值.
所成角的余弦值.
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)异面直线AC1与B1C所成角的余弦值为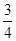 。
。
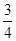 。
。(I)由题目条件可知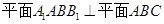 ,又因为
,又因为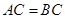 ,D为AB的中点,所以
,D为AB的中点,所以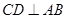 ,所以
,所以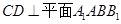 .
.
(II)连接BC1交B1C交于O点,连接OD,则OD//AC1,所以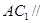 平面
平面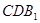 .
.
(III)在(I)的基础上可知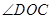 就是异面直线
就是异面直线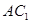 与
与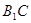 所成角,然后解三角形求角即可.
所成角,然后解三角形求角即可.
(Ⅰ)∵直三棱柱ABC—A1B1C1中
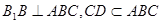 ,
,
∴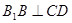 …………1
…………1
又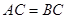 ,
,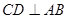 …………2
…………2
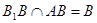 ………………………3
………………………3
∴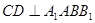 ……………………4
……………………4
(Ⅱ)设CB1与C1B的交点为E,连结DE,…………….5
∵D是AB的中点,E是BC1的中点,
∴DE//AC1,…………………………………………7
∵DE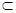 平面CDB1,AC1
平面CDB1,AC1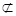 平面CDB1,………….8
平面CDB1,………….8
∴AC1//平面CDB1……………………………………9
(Ⅲ)∵DE//AC1,∴∠CED或其补角为AC1与B1C所成的角……..10
在△CED中,ED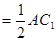 =
=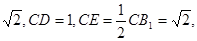 -------------12
-------------12
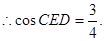
∴异面直线AC1与B1C所成角的余弦值为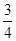 ………………………14
………………………14
 ,又因为
,又因为 ,D为AB的中点,所以
,D为AB的中点,所以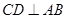 ,所以
,所以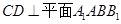 .
.(II)连接BC1交B1C交于O点,连接OD,则OD//AC1,所以
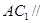 平面
平面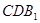 .
.(III)在(I)的基础上可知
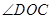 就是异面直线
就是异面直线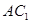 与
与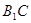 所成角,然后解三角形求角即可.
所成角,然后解三角形求角即可.(Ⅰ)∵直三棱柱ABC—A1B1C1中
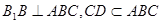 ,
,∴
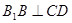 …………1
…………1又
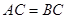 ,
,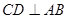 …………2
…………2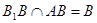 ………………………3
………………………3∴
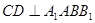 ……………………4
……………………4(Ⅱ)设CB1与C1B的交点为E,连结DE,…………….5
∵D是AB的中点,E是BC1的中点,
∴DE//AC1,…………………………………………7
∵DE
 平面CDB1,AC1
平面CDB1,AC1 平面CDB1,………….8
平面CDB1,………….8∴AC1//平面CDB1……………………………………9
(Ⅲ)∵DE//AC1,∴∠CED或其补角为AC1与B1C所成的角……..10
在△CED中,ED
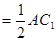 =
=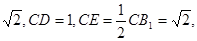 -------------12
-------------12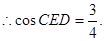
∴异面直线AC1与B1C所成角的余弦值为
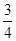 ………………………14
………………………14
练习册系列答案
相关题目
 中,
中,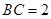 ,
,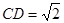 ,
,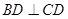 ,正方形
,正方形 所在平面与平面
所在平面与平面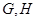 分别是
分别是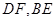 的中点。
的中点。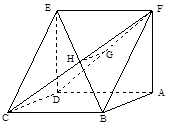
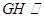 平面
平面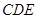 ;
;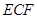 与平面
与平面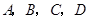 为空间四点.在
为空间四点.在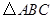 中,
中,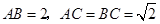 .等边三角形
.等边三角形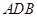 以
以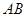 为轴运动.
为轴运动.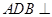 平面
平面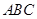 时,求
时,求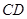 ;
;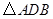 转动时,证明总有
转动时,证明总有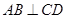 ?
?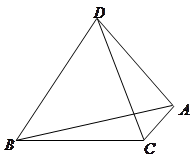
 中,
中, 为底面
为底面 的中心,
的中心,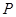 是
是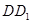 的中点,设
的中点,设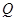 是
是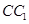 上的中点,求证:(1)
上的中点,求证:(1)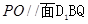 ;
;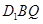 ∥平面
∥平面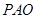 .
.
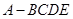 中,底面
中,底面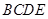 为矩形,侧面
为矩形,侧面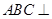 底面
底面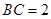 ,
,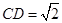 ,
,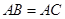 .
.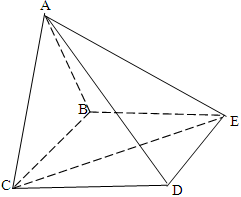
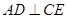 ;
; 与平面
与平面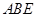 所成的角为
所成的角为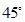 ,
, 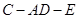 的余弦值.
的余弦值.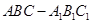 中,
中,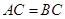 ,点
,点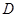 是
是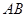 的中点,
的中点,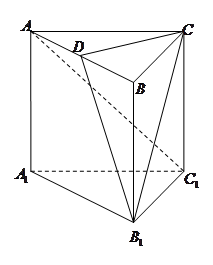
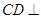 平面
平面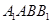 ;
;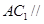 平面
平面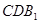
 、
、 和直线
和直线 、
、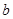 ,若
,若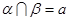 ,
,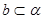 且
且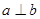 ,则
,则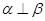 .
.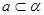 ,
,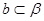 且
且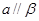 ,
,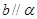 ,则
,则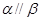 .
.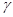 和直线
和直线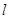 ,若
,若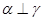 ,
,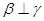 且
且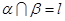 ,则
,则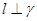 .
.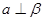 ,则
,则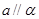 .
.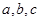 是三条不同的直线,
是三条不同的直线,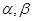 是两个不同的平面,则能使
是两个不同的平面,则能使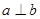 成立是( )
成立是( )