题目内容
有甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40km的B处，乙厂到河岸的垂足D与A相距50km，两厂要在此岸边合建一个供水站C，从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元，问供水站C建在岸边何处才能使水管费用最省？
根据题意知，只有点C在线段AD上某一适当位置，才能使总运费最省，设C点距D点x km，则
又设总的水管费用为y元，依题意有
．令
，解得
在（0，50）上，y只有一个极值点，根据实际问题的意义，
函数在
（km）处取得最小值，此时
（km）．
∴供水站建在A、D之间距甲厂20km处，可使水管费用最省．
解析:
根据题设条件作出图形，分析各已知条件之间的关系，借助图形的特征，合理选择这些条件间的联系方式，适当选定变元，构造相应的函数关系，通过求导的方法或其他方法求出函数的最小值，可确定点C的位置．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
相关题目
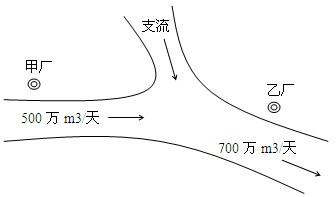如图，某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂，其中甲厂每天向河道内排放污水2万m3，每天流过甲厂的河水流量是500万m3（含甲厂排放的污水）；乙厂每天向河道内排放污水1.4万m3，每天流过乙厂的河水流量是700万m3（含乙厂排放的污水）．由于两厂之间有一条支流的作用，使得甲厂排放的污水在流到乙厂时，有20%可自然净化．假设工厂排放的污水能迅速与河水混合，且甲厂上游及支流均无污水排放．根据环保部门的要求，整个河流中污水含量不能超过0.2%，为此，甲、乙两个工厂都必须各自处理一部分污水．
某工厂有甲、乙两个车间，每个车间各有编号为1、2、3、4、5的5名技工．在某天内每名技工加工的合格零件的个数如下表：
| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲车间 | 4 | 5 | 7 | 9 | 10 |
| 乙车间 | 5 | 6 | 7 | 8 | 9 |
（Ⅱ）质检部门从甲、乙两个车间中各随机抽取1名技工，对其加工的零件进行检测，若两人完成合格零件个数之和不小于12个，则称该工厂“质量合格”，求该工厂“质量合格”的概率．