题目内容
18.两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )| A. | akm | B. | $\sqrt{2}$akm | C. | 2akm | D. | $\sqrt{3}$akm |
分析 先根据题意确定∠ACB的值,再由余弦定理可直接求得|AB|的值.
解答  解:根据题意,
解:根据题意,
△ABC中,∠ACB=180°-20°-40°=120°,
∵AC=BC=akm,
∴由余弦定理,得cos120°=$\frac{{a}^{2}+{a}^{2}-A{B}^{2}}{2×a×a}$,
解之得AB=$\sqrt{3}$akm,
即灯塔A与灯塔B的距离为$\sqrt{3}$akm,
故选:D.
点评 本题给出实际应用问题,求海洋上灯塔A与灯塔B的距离.着重考查了三角形内角和定理和运用余弦定理解三角形等知识,属于基础题.

练习册系列答案
相关题目
8.复数z=$\frac{{{{(1+i)}^2}}}{1-i}$的共轭复数$\overline{z}$=( )
| A. | 1+i | B. | -1+i | C. | -1-i | D. | 1-i |
6.已知z=$\frac{2+i}{1-2i}$,则|z|+z=( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
13.已知sin($\frac{π}{6}-α$)=$\frac{1}{3}$,则sin($\frac{π}{6}+2α$)=( )
| A. | -$\frac{2\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{2}}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
5.下列说法中,正确的是( )
| A. | ?α,β∈R,sin(α+β)≠sinα+sinβ | |
| B. | 命题p:?x∈R,x2-x>0,则?p:?x∈R,x2-x<0 | |
| C. | 在△ABC中,“$\overrightarrow{AB}•\overrightarrow{AC}>0$”是“△ABC为锐角三角形”的必要不充分条件 | |
| D. | 已知x∈R,则“x>1”是“x>2”成立的充分不必要条件 |
 和点
和点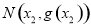 分别是函数
分别是函数 和
和 图象上的点,且
图象上的点,且 ,若直线
,若直线 轴,则
轴,则 两点间的距离的最小值为( )
两点间的距离的最小值为( ) B.
B.
 D.
D.