题目内容
在直角梯形ABCD中,AB∥CD,∠DAB=∠ADC=
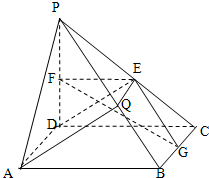
、AB=AD=2CD=4,作MN∥AB,连接AC交MN于P,现沿MN将直角梯形ABCD折成直二面角
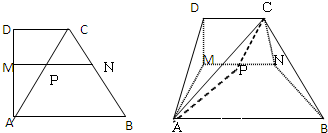
(I)若M为AD中点时,求异面直线MN与AC所成角;
(Ⅱ)证明:当MN在直角梯形内保持MN∥AB作平行移动时,折后所成∠APC大小不变;
(Ⅲ)当点M在怎样的位置时,点M到面ACD的距离最大?并求出这个最大值.
| π | 2 |

(I)若M为AD中点时,求异面直线MN与AC所成角;
(Ⅱ)证明:当MN在直角梯形内保持MN∥AB作平行移动时,折后所成∠APC大小不变;
(Ⅲ)当点M在怎样的位置时,点M到面ACD的距离最大?并求出这个最大值.
分析:(I)MN∥DC,DC⊥平面ADM,则∠ACD为异面直线MN与AC所成角,利用正切函数,可得结论;
(II)利用余弦定理,可求∠APC大小;
(Ⅲ)由题意,平面ACD⊥平面AMD,则过M作ME⊥AD,ME⊥平面ACD,故ME为点M到面ACD的距离,利用等面积,即可求解.
(II)利用余弦定理,可求∠APC大小;
(Ⅲ)由题意,平面ACD⊥平面AMD,则过M作ME⊥AD,ME⊥平面ACD,故ME为点M到面ACD的距离,利用等面积,即可求解.
解答: (I)解:由题意,MN∥DC,DC⊥平面ADM,则∠ACD为异面直线MN与AC所成角
(I)解:由题意,MN∥DC,DC⊥平面ADM,则∠ACD为异面直线MN与AC所成角
∵DM=AM=2,DM⊥AM
∴AD=2
∴tan∠ACD=
∴∠ACD=arctan
;
(II)证明:设MP=a,则AM=2a,DM=4-2a,
∴AP=
a,PC=
=
,AC=
=
∴cos∠APC=
=-
为定值,
∴MN在直角梯形内保持MN∥AB作平行移动时,折后所成∠APC大小不变;
(Ⅲ)解:由题意,平面ACD⊥平面AMD,则过M作ME⊥AD,ME⊥平面ACD,
∴ME为点M到面ACD的距离
由(II)知,ME=
=
令t=2a(2-a),则1≥t>0,ME=
=
=
∴t=1时,ME取得最大值
,此时M是AD的中点.
 (I)解:由题意,MN∥DC,DC⊥平面ADM,则∠ACD为异面直线MN与AC所成角
(I)解:由题意,MN∥DC,DC⊥平面ADM,则∠ACD为异面直线MN与AC所成角∵DM=AM=2,DM⊥AM
∴AD=2
| 2 |
∴tan∠ACD=
| 2 |
∴∠ACD=arctan
| 2 |
(II)证明:设MP=a,则AM=2a,DM=4-2a,
∴AP=
| 5 |
| (2-a)2+(4-2a)2 |
| 5a2-20a+20 |
| 4a2+(4-2a)2+4 |
| 8a2-16a+20 |
∴cos∠APC=
| 5a2+5a2-20a+20-8a2+16a-20 | ||||
2
|
| 1 |
| 5 |
∴MN在直角梯形内保持MN∥AB作平行移动时,折后所成∠APC大小不变;
(Ⅲ)解:由题意,平面ACD⊥平面AMD,则过M作ME⊥AD,ME⊥平面ACD,
∴ME为点M到面ACD的距离
由(II)知,ME=
| 2a(4-2a) | ||
|
| 2a(2-a) | ||
|
令t=2a(2-a),则1≥t>0,ME=
| t | ||
|
| 1 | ||||||
|
| 1 | ||||||||
|
∴t=1时,ME取得最大值
| ||
| 5 |
点评:本题考查空间角与空间距离的计算,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
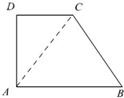
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为