题目内容
已知M=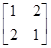 ,β=
,β=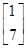 ,计算M5β.
,计算M5β.
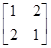 ,β=
,β=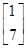 ,计算M5β.
,计算M5β.
矩阵M的特征多项式为f(λ)= =λ2-2λ-3.
=λ2-2λ-3.
令f(λ)=0,解得λ1=3,λ2=-1,从而求得对应的一个特征向量分别为α1= ,α2=
,α2= .
.
令β=mα1+nα2,则m=4,n=-3.
M5β=M5(4α1-3α2)=4(M5α1)-3(M5α2)=4( α1)-3(
α1)-3( α2)
α2)
=4×35 -3×(-1)5
-3×(-1)5 =
= .
.
 =λ2-2λ-3.
=λ2-2λ-3.令f(λ)=0,解得λ1=3,λ2=-1,从而求得对应的一个特征向量分别为α1=
 ,α2=
,α2= .
.令β=mα1+nα2,则m=4,n=-3.
M5β=M5(4α1-3α2)=4(M5α1)-3(M5α2)=4(
 α1)-3(
α1)-3( α2)
α2)=4×35
 -3×(-1)5
-3×(-1)5 =
= .
.
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 (k≠0)的一个特征向量为α=
(k≠0)的一个特征向量为α= ,A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1).求实数a,k的值.
,A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1).求实数a,k的值. ,
, ,计算
,计算 .
.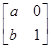 (a>0)对应的变换作用下得到的曲线为x2+y2=1.
(a>0)对应的变换作用下得到的曲线为x2+y2=1.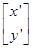 =
=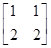
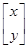 下,直线x+y=k(k为常数)上的所有点都变为一个点,求此点坐标.
下,直线x+y=k(k为常数)上的所有点都变为一个点,求此点坐标. .
.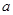 、
、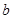 、
、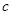 是
是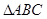 的三边长,且满足
的三边长,且满足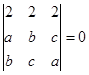 ,则
,则 的特征多项式.
的特征多项式.