题目内容
设关于x的不等式ax2+8(a+1)x+7a+16≥0最多有6个整数解,且0是其中一个解,则整数a的值为________.
-2
分析:先确定a<0,再利用0为其中的一个解,a∈Z,求出a的值,从而可得不等式,由最多有6个整数解,可得整数a的值.
解答:设y=ax2+8(a+1)x+7a+16,其图象为抛物线.
对于任意一个给定的a值其抛物线只有在开口向下的情况下才能满足y≥0而整数解只有有限个,所以a<0.
因为0为其中的一个解可以求得a≥- ,又a∈Z,所以a=-2,-1,
,又a∈Z,所以a=-2,-1,
则原不等式为-2x2-8x+2≥0与-x2+9≥0,分别求解得- -2≤x≤
-2≤x≤ -2和-3≤x≤3,
-2和-3≤x≤3,
∵x为整数,
∴x=-4,-3,-2,-1,0和x=-3,-2,-1,0,1,2,3
又不等式ax2+8(a+1)x+7a+16≥0最多有6个整数解,
∴a=-2.
故答案为:-2.
点评:本题考查一元二次不等式的应用,解题的关键是确定a的值,求出相应一元二次不等式的解集.
分析:先确定a<0,再利用0为其中的一个解,a∈Z,求出a的值,从而可得不等式,由最多有6个整数解,可得整数a的值.
解答:设y=ax2+8(a+1)x+7a+16,其图象为抛物线.
对于任意一个给定的a值其抛物线只有在开口向下的情况下才能满足y≥0而整数解只有有限个,所以a<0.
因为0为其中的一个解可以求得a≥-
 ,又a∈Z,所以a=-2,-1,
,又a∈Z,所以a=-2,-1,则原不等式为-2x2-8x+2≥0与-x2+9≥0,分别求解得-
 -2≤x≤
-2≤x≤ -2和-3≤x≤3,
-2和-3≤x≤3,∵x为整数,
∴x=-4,-3,-2,-1,0和x=-3,-2,-1,0,1,2,3
又不等式ax2+8(a+1)x+7a+16≥0最多有6个整数解,
∴a=-2.
故答案为:-2.
点评:本题考查一元二次不等式的应用,解题的关键是确定a的值,求出相应一元二次不等式的解集.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
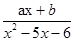 >0的解集为________.
>0的解集为________.