题目内容
已知△ABC的面积为2，在△ABC所在的平面内有两点P、q，满足
，
=2
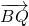，则△APQ的面积为
- A.
- B.
- C.1
- D.2
B
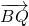分析：画出△ABC，通过足，=2，标出满足题意的P、Q位置，利用三角形的面积公式求解即可．
解答：
解：由题意可知，P为AC的中点，=2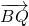，可知Q为AB的一个三等分点，如图：
因为S△ABC=
=2．
所以S△APQ=
=
=．
故选B．
点评：本题考查向量在几何中的应用，三角形的面积的求法，考查转化思想与计算能力．
分析：画出△ABC，通过足
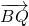，=2，标出满足题意的P、Q位置，利用三角形的面积公式求解即可．解答：
解：由题意可知，P为AC的中点，=2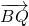，可知Q为AB的一个三等分点，如图：因为S△ABC=
=2．所以S△APQ=
==．故选B．
点评：本题考查向量在几何中的应用，三角形的面积的求法，考查转化思想与计算能力．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
如图，已知△ABC的面积为14，D、E分别为边AB、BC上的点，且AD：DB=BE：EC=2：1，AE与CD交于P．设存在λ和μ使
（2012•温州一模）如图，在△ABC中，AD⊥BC，垂足为D，且BD：DC：AD=2：3：6．