Question

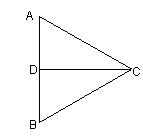
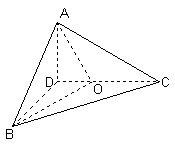
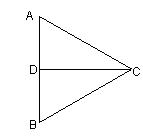
如图，已知CD是等边三角形ABC边AB上的高，沿CD将△ADC折起，使平面ADC与平面BDC互相垂直

   （Ⅰ）求AB与平面BDC所成的角；

   （Ⅱ）若O点在DC上，且分DC的比为，求二面角A-BO-C的正切值.

 

Answer 1

答案：
解析：

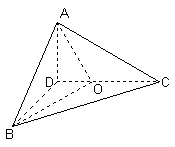
答案：（Ⅰ）解：∵  A-DC-B为直二面角，且AD⊥DC. ∴  AD⊥平面BDC ∴  AB与平面BDC所成的角为∠ABD ∵  AD=BD，∠ADB=90° ∴  ∠ABD=45° ∴  AB与平面BDC所成的角为45°.   （Ⅱ）解：如图，过D作BO的垂线交BO于H，并延长交BC于G，连AH，AG ∵   AD⊥平面BDC，又DH⊥BO ∴   BO⊥AH（三垂线定理） ∴   ∠AHG为二面角A-BO-G的平面角 ∵　点O在DC上，且，则 ∴   ∠DBO=30° ∴   BD=2DH 即   AD=2DH　　        在Rt△ADH中， ∴   tan∠AHG=tan（π－∠AHD）= －2 故二面角A-BO-C的正切值为－2.