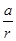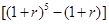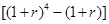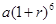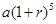题目内容
(本小题满分12分)已知函数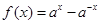 ,
,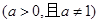 ,
,
(1) 判断函数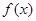 的奇偶性,并证明;
的奇偶性,并证明;
(2) 判断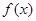 的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
(3) 若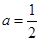 ,方程
,方程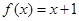 是否有根?如果有根
是否有根?如果有根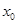 ,请求出一个长度为1的区间
,请求出一个长度为1的区间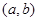 ,使
,使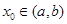 ;如果没有,请说明理由。(注:区间
;如果没有,请说明理由。(注:区间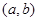 的长度=
的长度=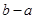 )
)
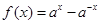 ,
,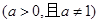 ,
,(1) 判断函数
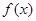 的奇偶性,并证明;
的奇偶性,并证明;(2) 判断
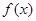 的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)(3) 若
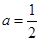 ,方程
,方程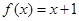 是否有根?如果有根
是否有根?如果有根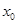 ,请求出一个长度为1的区间
,请求出一个长度为1的区间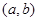 ,使
,使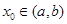 ;如果没有,请说明理由。(注:区间
;如果没有,请说明理由。(注:区间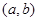 的长度=
的长度=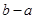 )
)(1) 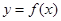 为奇函数,证明:见解析;
为奇函数,证明:见解析;
(2)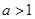 时,
时,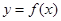 单调递增;
单调递增;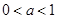 ,
,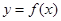 单调递减。
单调递减。
(3)方程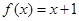 有根
有根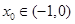 。
。
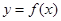 为奇函数,证明:见解析;
为奇函数,证明:见解析;(2)
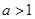 时,
时,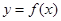 单调递增;
单调递增;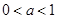 ,
,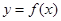 单调递减。
单调递减。(3)方程
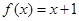 有根
有根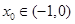 。
。试题分析:(1)根据f(-x)=-f(x)可知此函数是奇函数。
(2) 分a>1和0<a<1两种情况研究即可。a>1时,是两个增函数的和,0<a<1时,是两个减函数的和。
从而确定其单调性与底数a有关系。
(3) 当
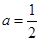 ,
,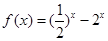 ,又
,又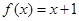 ,再令
,再令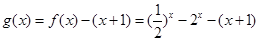 ,
,然后判断g(-1),g(0)的值,从而判断y=g(x)在(-1,0)上是否存在零点,从而达到证明f(x)=x+1是否在(-1,0)上有根的目的。
(1)
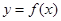 为奇函数……………………1分
为奇函数……………………1分证明:∵
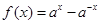 的定义域为R,关于原点对称 …………………2分
的定义域为R,关于原点对称 …………………2分又
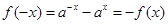 …………………………………………3分
…………………………………………3分所以可知
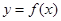 为奇函数……………………………………………4分
为奇函数……………………………………………4分(2) ∵
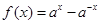 =
=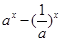
① 当
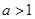 时,
时,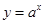 单调递增,
单调递增,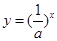 单调递减,
单调递减,所以
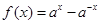 单调递增…………………………………………………6分
单调递增…………………………………………………6分②当
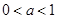 时,
时,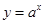 单调递减,
单调递减,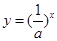 单调递增,
单调递增,所以
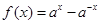 单调递减。
单调递减。综上可知
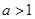 时,
时,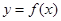 单调递增;
单调递增;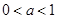 ,
,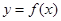 单调递减。
单调递减。………………………………………………8分
(3)当
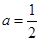 ,
,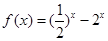 ,又
,又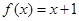
设
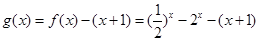 …………………………………9分
…………………………………9分∵
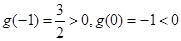 ………………………………………………10分
………………………………………………10分∴
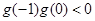 ,故
,故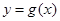 存在零点
存在零点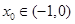
即方程
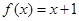 有根
有根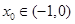 ……………………………………………12分
……………………………………………12分点评:掌握判断函数奇偶性的方法:一要看定义域是否关于原点对称,二要看f(-x)与f(x)的关系。
要掌握函数单调性的定义,它是证明抽象函数单调性的依据。函数的零点与方程的根的关系要搞清楚,它是实现根与零点的判断转化的依据。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 _________
_________ 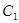 的方程是
的方程是
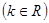 ,曲线
,曲线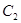 的方程是
的方程是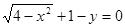 ,给出下列结论:
,给出下列结论: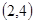 ;
;  ②曲线
②曲线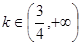 时,
时,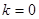 时,则
时,则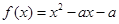 ,
,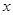 ,使得
,使得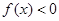 ,求实数
,求实数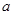 的取值范围;
的取值范围;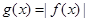 ,且
,且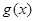 在区间
在区间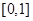 上单调递增,求实数
上单调递增,求实数 中,满足对任意
中,满足对任意 ,
,
 (0,
(0, )且
)且 ,都有
,都有 的是 ( )
的是 ( ) 



 在下列哪个区间内有零点
在下列哪个区间内有零点 



 (月)的函数图象如图所示,则这个工厂对这种产品来说( )
(月)的函数图象如图所示,则这个工厂对这种产品来说( )
 元(一年定期),若年利率为
元(一年定期),若年利率为 保持不变,且每年到期存款和利息自动转为新的一年定期,到2011年底将所有存款及利息全部取回,则可取回的钱数(元)为
保持不变,且每年到期存款和利息自动转为新的一年定期,到2011年底将所有存款及利息全部取回,则可取回的钱数(元)为