题目内容
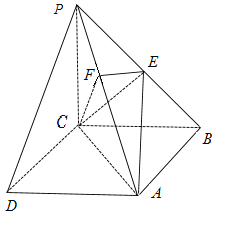
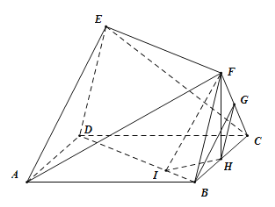
【题目】如图，已知多面体
，其底面
为矩形，四边形
为平行四边形，平面
平面，
，
，
是
的中点.
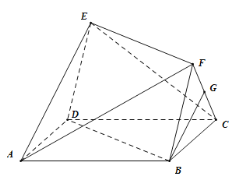
（1）证明：
平面
；
（2）求直线
与平面所成角的余弦值.
【答案】（1）证明见详解；（2）
【解析】
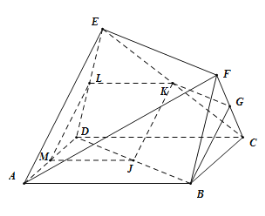
（1）取
中点
，
的中点
，
的中点
，
的中点
，推到出四边形
是平行四边形，从而
，推到出四边形
是平行四边形，从而
，
，由此能证明
平面
.
（2）直线
与平面
所成角即等于直线
与平面所成角，作
，
，连接
，则
平面，从而
点到平面的距离等于
点平面的距离
，由等面积法求出
，由此能求出直线与平面所成角的余弦值.
（1）取中点，的中点，的中点，的中点，
，
，
四边形是平行四边形，
，
，
，
四边形是平行四边形，
，
，
平面，
平面，
平面
（2）由（1）知，
直线与平面所成角，
即等于直线与平面所成角，
作，，连接，
都是所在棱的中点，
平面，
点到平面的距离等于点平面的距离，
，
，
，
由等面积法可知：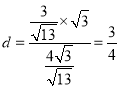
，
，
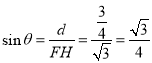直线与平面所成角的余弦值为
.
轻松夺冠全能掌控卷系列答案
【题目】法国数学家庞加是个喜欢吃面包的人，他每天都会购买一个面包，面包师声称自己出售的每个面包的平均质量是1000
，上下浮动不超过50.这句话用数学语言来表达就是：每个面包的质量服从期望为1000，标准差为50的正态分布.
（1）假设面包师的说法是真实的，从面包师出售的面包中任取两个，记取出的两个面包中质量大于1000的个数为
，求的分布列和数学期望；
（2）作为一个善于思考的数学家，庞加莱每天都会将买来的面包称重并记录，25天后，得到数据如下表，经计算25个面包总质量为24468.庞加莱购买的25个面包质量的统计数据（单位：）
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
尽管上述数据都落在
上，但庞加菜还是认为面包师撒谎，根据所附信息，从概率角度说明理由
附：
①若
，从X的取值中随机抽取25个数据，记这25个数据的平均值为Y，则由统计学知识可知：随机变量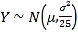
②若
，则
，
，
；
③通常把发生概率在0.05以下的事件称为小概率事件.
