题目内容
函数
，x∈[0，π]的图象绕x轴旋转一周，得到一旋转体，该旋转体的体积为
- A.1
- B.2
- C.π
- D.2π
D
分析：根据旋转体的体积公式和微积分的几何意义，并结合积分计算公式加以计算，即可算出该旋转体的体积．
解答：由旋转体的体积公式和微积分的几何意义，得旋转体的体积为
V=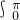
π（
）2dx=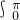πsinxdx=-cosx
=π（-cosπ+cos0）=2π
故选：D
点评：本题给出函数y=的图象，求它在区间上的部分绕x轴旋转一周得到一旋转体的体积．着重考查了据旋转体的体积公式、微积分的几何意义和积分计算公式等知识，属于中档题．
分析：根据旋转体的体积公式和微积分的几何意义，并结合积分计算公式加以计算，即可算出该旋转体的体积．
解答：由旋转体的体积公式和微积分的几何意义，得旋转体的体积为
V=
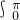π（）2dx=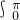πsinxdx=-cosx=π（-cosπ+cos0）=2π故选：D
点评：本题给出函数y=
的图象，求它在区间上的部分绕x轴旋转一周得到一旋转体的体积．着重考查了据旋转体的体积公式、微积分的几何意义和积分计算公式等知识，属于中档题． 
练习册系列答案
相关题目
函数f（x），g（x）的图象分别如右图1、2所示．函数h（x）=f（x）+g（x）．则以下有关函数h（x）的性质中，错误的是（ ）