题目内容
如图,已知椭圆 内有一点M,过M作两条动直线AC、BD分别交椭圆于A、C和B、D两点,若
内有一点M,过M作两条动直线AC、BD分别交椭圆于A、C和B、D两点,若 .
.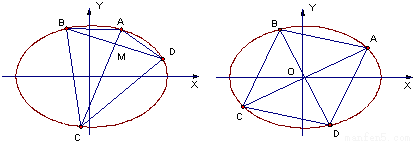
(1)证明:AC⊥BD;
(2)若M点恰好为椭圆中心O
(i)四边形ABCD是否存在内切圆?若存在,求其内切圆方程;若不存在,请说明理由.
(ii)求弦AB长的最小值.
【答案】分析:(1)设出点的坐标,利用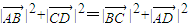 ,即可证得
,即可证得 ,从而AC⊥BD;
,从而AC⊥BD;
(2)(i)根据AC⊥BD,由椭圆对称性知AC与BD互相平分,所以四边形ABCD是菱形,它存在内切圆,设直线AB方程为:y=kx+m,利用圆心到直线的距离,可得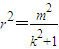 ;联立
;联立 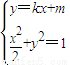 ,利用OA⊥OB,可得
,利用OA⊥OB,可得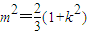 ,从而可求内切圆的方程;
,从而可求内切圆的方程;
(ii)求出弦AB的长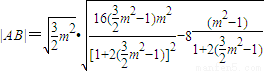 =
=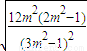 ,令3m2-1=t,则
,令3m2-1=t,则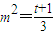 ,所以
,所以 根据
根据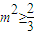 ,即可求得弦AB长的最小值.
,即可求得弦AB长的最小值.
解答:(1)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)
由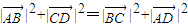 知
知
展开整理得:x1x2+y1y2+x3x4+y3y4=x2x3+y2y3+x1x4+y1y4
即x1(x2-x4)+x3(x4-x2)+y1(y2-y4)+y3(y4-y2)=0
∴(x1-x3)(x2-x4)+(y1-y3)(y2-y4)=0
即 ,
,
∴AC⊥BD….(4分)
(2)解:(i)∵AC⊥BD,由椭圆对称性知AC与BD互相平分,
∴四边形ABCD是菱形,它存在内切圆,圆心为O,设半径为r,直线AB方程为:y=kx+m
则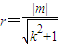 ,即
,即 ①
①
联立 得(1+2k2)x2+4kmx+2m2-2=0
得(1+2k2)x2+4kmx+2m2-2=0
∴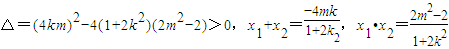
由(1)知OA⊥OB,
∴x1x2+y1y2=0,即x1x2+(kx1+m)(kx2+m)=0
∴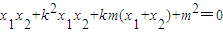
∴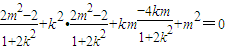
∴2m2-2+2m2k2-2k2-4k2m2+m2+2m2k2=0
∴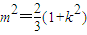 ②
②
②代入①有: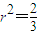
∴存在内切圆,其方程为: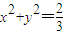 ….(9分)
….(9分)
容易验证,当k不存在时,上述结论仍成立.
(ii)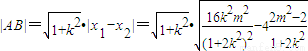
∵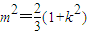

∴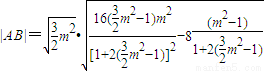 =
=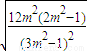
令3m2-1=t,则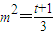
∴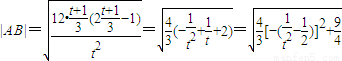
∵ ,∴
,∴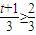 ,故t≥1,∴
,故t≥1,∴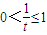
当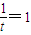 时,
时,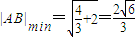 ,此时
,此时
容易验证,当k不存在时,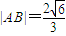 ….(13分)
….(13分)
点评:本题以椭圆方程为载体,考查向量知识的运用,考查椭圆与圆的综合,考查圆中的弦长的求解,挖掘隐含,熟练计算是关键.
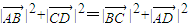 ,即可证得
,即可证得 ,从而AC⊥BD;
,从而AC⊥BD;(2)(i)根据AC⊥BD,由椭圆对称性知AC与BD互相平分,所以四边形ABCD是菱形,它存在内切圆,设直线AB方程为:y=kx+m,利用圆心到直线的距离,可得
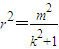 ;联立
;联立 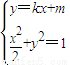 ,利用OA⊥OB,可得
,利用OA⊥OB,可得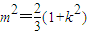 ,从而可求内切圆的方程;
,从而可求内切圆的方程;(ii)求出弦AB的长
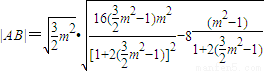 =
=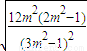 ,令3m2-1=t,则
,令3m2-1=t,则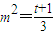 ,所以
,所以 根据
根据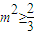 ,即可求得弦AB长的最小值.
,即可求得弦AB长的最小值.解答:(1)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)
由
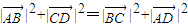 知
知
展开整理得:x1x2+y1y2+x3x4+y3y4=x2x3+y2y3+x1x4+y1y4
即x1(x2-x4)+x3(x4-x2)+y1(y2-y4)+y3(y4-y2)=0
∴(x1-x3)(x2-x4)+(y1-y3)(y2-y4)=0
即
 ,
,∴AC⊥BD….(4分)
(2)解:(i)∵AC⊥BD,由椭圆对称性知AC与BD互相平分,
∴四边形ABCD是菱形,它存在内切圆,圆心为O,设半径为r,直线AB方程为:y=kx+m
则
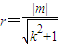 ,即
,即 ①
①联立
 得(1+2k2)x2+4kmx+2m2-2=0
得(1+2k2)x2+4kmx+2m2-2=0∴
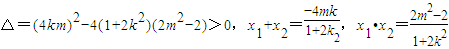
由(1)知OA⊥OB,
∴x1x2+y1y2=0,即x1x2+(kx1+m)(kx2+m)=0
∴
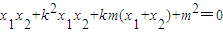
∴
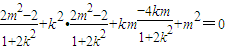
∴2m2-2+2m2k2-2k2-4k2m2+m2+2m2k2=0
∴
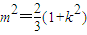 ②
②②代入①有:
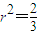
∴存在内切圆,其方程为:
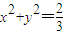 ….(9分)
….(9分)容易验证,当k不存在时,上述结论仍成立.
(ii)
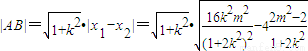
∵
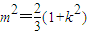

∴
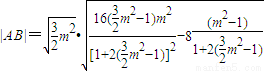 =
=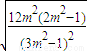
令3m2-1=t,则
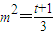
∴
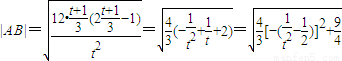
∵
 ,∴
,∴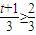 ,故t≥1,∴
,故t≥1,∴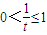
当
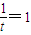 时,
时,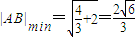 ,此时
,此时
容易验证,当k不存在时,
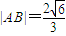 ….(13分)
….(13分)点评:本题以椭圆方程为载体,考查向量知识的运用,考查椭圆与圆的综合,考查圆中的弦长的求解,挖掘隐含,熟练计算是关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为
如图,已知AB=2c(常数c>0),以AB为直径的圆有一内接梯形ABCD,且AB∥CD,若椭圆以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,椭圆的离心率为