题目内容
已知椭圆 与直线l:mx-y-m=0
与直线l:mx-y-m=0(1)求证:对于m∈R,直线l与椭圆C总有两个不同的交点;
(2)设直线l与椭圆C交于A、B两点,若|AB|=
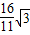 ,求直线l的倾斜角.
,求直线l的倾斜角.
【答案】分析:(1)分m=0和m≠0两种情况分别判断直线和椭圆C的位置关系即可.m≠0时,联立直线方程与椭圆方程根据判别式和0的关系即可得到结论.
(2)联立直线方程与椭圆方程,再结合韦达定理以及弦长公式即可解决问题.
解答:解:(1)证明:1、当m=0,直线方程y=1,与圆有两个交点,符合题意
2、当m≠0,将椭圆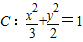 与直线l:mx-y-m=0联立得
与直线l:mx-y-m=0联立得
(3m2+2)x2-6m2x+3m2-6=0
△=(6m2)2-4(3m2+2)×(3m2-6)=48m2+48>0,符合题意
∴对于m∈R,直线l与椭圆C总有两个不同的交点
(2)设A、B的坐标分别为(x1,y1)、(x2,y2),
则x1+x2= x1•x2=
x1•x2=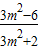 |AB|=
|AB|=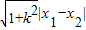
=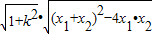
=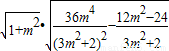 =
=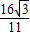
解得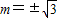 ∴l的倾斜角为
∴l的倾斜角为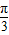 或
或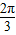
点评:解决此类问题的关键是熟练掌握椭圆有关数值之间的关系,以及椭圆与直线的位置关系并且结合韦达定理解决问题.
(2)联立直线方程与椭圆方程,再结合韦达定理以及弦长公式即可解决问题.
解答:解:(1)证明:1、当m=0,直线方程y=1,与圆有两个交点,符合题意
2、当m≠0,将椭圆
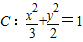 与直线l:mx-y-m=0联立得
与直线l:mx-y-m=0联立得(3m2+2)x2-6m2x+3m2-6=0
△=(6m2)2-4(3m2+2)×(3m2-6)=48m2+48>0,符合题意
∴对于m∈R,直线l与椭圆C总有两个不同的交点
(2)设A、B的坐标分别为(x1,y1)、(x2,y2),
则x1+x2=
 x1•x2=
x1•x2=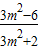 |AB|=
|AB|=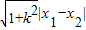
=
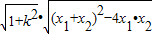
=
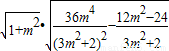 =
=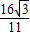
解得
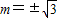 ∴l的倾斜角为
∴l的倾斜角为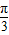 或
或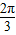
点评:解决此类问题的关键是熟练掌握椭圆有关数值之间的关系,以及椭圆与直线的位置关系并且结合韦达定理解决问题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
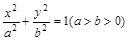 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且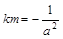 .
.
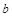 的值;
的值;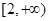 ,使得四边形OACB是平行四边形,请证明你的结论;
,使得四边形OACB是平行四边形,请证明你的结论; 及直线l:y=x+m.
及直线l:y=x+m. 及直线l:y=
及直线l:y= x+m。
x+m。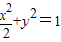 及直线l:y=x+m.
及直线l:y=x+m.