题目内容
若条件p:
≥1,条件q:2x+3≥x2,则?p是?q的( )
| 1-x |
| 1+x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
分析:先通过解分式不等式化简条件p,通过解二次不等式化简条件q,求出¬p,¬q,根据数集的范围大小,判断出¬p是¬q的必要不充分条件.
解答:解:命题p:
≥1即为-1<x≤0
∴¬p:x≤-1或x>0
条件q:2x+3≥x2即为-1≤x≤3
∴¬q:x<-1或x>3
∴¬p是¬q的必要不充分条件.
| 1-x |
| 1+x |
∴¬p:x≤-1或x>0
条件q:2x+3≥x2即为-1≤x≤3
∴¬q:x<-1或x>3
∴¬p是¬q的必要不充分条件.
点评:判断一个命题是另一个命题的什么条件,一般先判断前者成立是否能推出后者成立,再判断后者成立能否推出前者成立,利用充要条件的定义加以判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
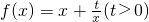 和点P(1,0),过点P作曲线y=f(x)的两条切线PM,PN,切点分别为M(x1,y1),N(x2,y2).
和点P(1,0),过点P作曲线y=f(x)的两条切线PM,PN,切点分别为M(x1,y1),N(x2,y2).