题目内容

定义在区间[0，
π
ω
]上的函数y=2sinωx（ω＞0）截直线y=1所得的弦长为2，则ω=______．
设直线y=1与函数y=2sin2ωx在区间[0，
π
ω
]上的交点为M（x1，
1
2
），N（x2，
1
2
），
则x2-x1=2；
∵sin2ωx=
1
2
，x∈[0，
π
ω
]，
∴2ωx2=
5π
6
，2ωx1=
π
6
，
∴2ωx2-2ωx1=2ω（x2-x1）=4ω=
2π
3
，
∴ω=
π
6
．
故答案为：
π
6
练习册系列答案
相关题目
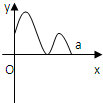
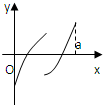
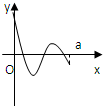
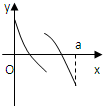
精英家教网已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1、x2，给出下列结论：
①f（x2）-f（x1）＞x2-x1；
②x2f（x1）＞x1f（x2）；
③
f(x1)+f(x2)
2
＜f （
x1+x2
2
）．
其中正确结论的序号是
 
（把所有正确结论的序号都填上）．
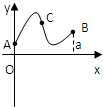精英家教网定义在区间[0，a]上的函数f（x）的图象如图所示，记以A（0，f（0）），B（a，f（a）），C（x，f（x））为顶点的三角形的面积为S（x），则函数S（x）的导函数S′（x）的图象大致是（　　）
A、精英家教网B、精英家教网C、精英家教网D、精英家教网
定义在区间[0，1]上的函数f（x）满足：f（0）=f（1）=0，且对任意的x1，x2∈[0，1]都有f（
x1+x2
2
）≤f（x1）+f（x2）；
（1）证明：对任意的x∈[0，1]，都有f（x）≥0；
（2）求f（
3
4
）的值．
已知定义在区间[0，2]上的两个函数f（x）和g（x），其中f（x）=x2-2ax+4，g（x）=
ax+1x+1
，（a≥0）
（1）求函数y=f（x）的最小值m（a）；
（2）讨论函数y=g（x）的单调性
（3）若对任意x1，x2∈[0，2]，f（x2）＞g（x1）恒成立，求a的取值范围．
已知定义在区间[0，2]上的两个函数f（x）和g（x），其中f（x）=x2-2ax+4（a≥1），g(x)=
2xx+1
．
（1）求函数y=f（x）的最小值m（a）及g（x）的值域；
（2）若对任意x1、x2∈[0，2]，f（x2）＞g（x1）恒成立，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网