题目内容
已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=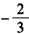 ,
,
(1)求证f(x)在R上是减函数;
(2)求f(x)在[-3,3]上的最大值和最小值.
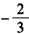 ,
,(1)求证f(x)在R上是减函数;
(2)求f(x)在[-3,3]上的最大值和最小值.
解:(1)由f(x)+f(y)=f(x+y)可得f(x+y)-f(x)=f(y),
在R上任取x1>x2,则f(x1)-f(x2)=f(x1-x2),
∵x1>x2,
∴x1-x2>0,
又∵x>0时,f(x)<0,
∴f(x1-x2)<0,即f(x1)-f(x2)<0,
由定义可知f(x)在R上为单调递减函数.
(2)∵f(x)在R上是减函数,
∴f(x)在[ -3,3]上也是减函数,
∴f(-3)最大,f(3)最小,
f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3×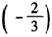 =-2,
=-2,
∴f(-3)=f(4-3)-f(4)=f(1)-f(3)-f(1)=-f(3)=2,
即f(x)在[-3,3]上的最大值为2,最小值为-2.
在R上任取x1>x2,则f(x1)-f(x2)=f(x1-x2),
∵x1>x2,
∴x1-x2>0,
又∵x>0时,f(x)<0,
∴f(x1-x2)<0,即f(x1)-f(x2)<0,
由定义可知f(x)在R上为单调递减函数.
(2)∵f(x)在R上是减函数,
∴f(x)在[ -3,3]上也是减函数,
∴f(-3)最大,f(3)最小,
f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3×
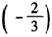 =-2,
=-2,∴f(-3)=f(4-3)-f(4)=f(1)-f(3)-f(1)=-f(3)=2,
即f(x)在[-3,3]上的最大值为2,最小值为-2.

练习册系列答案
相关题目
 .任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
.任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明). ;
; ;
; ,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).