题目内容
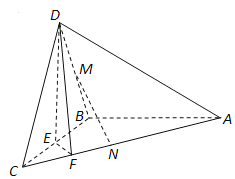
【题目】如图， 
分别是椭圆
的左、右焦点， 
是椭圆
的顶点， 
是直线
与椭圆
的另一个交点， 
.
（1）求椭圆
的离心率；
（2）已知
的面积为
，求
的值.
【答案】(1) 
；(2) 
.
【解析】试题分析：（1）由题意知
为等边三角形，从而得到
的关系式，进而求得离心率；（2）首先根据椭圆的性质得到
的关系式，然后设出直线
的方程，并代入椭圆方程得到
点坐标，从而求得
，再根据三角形面积公式求得
的值，进而求得椭圆的方程；别解：设
，然后利用椭圆的定义表示出
的长，再利用余弦定理得到
的关系式，从而根据三角形面积公式求得
的值，进而求得椭圆的方程.
试题解析：
（1）由题意可知， 
为等边三角形， 
，所以
.
（2）（ 方法一）
， 
.
直线
的方程可为
．
将其代入椭圆方程
，得
所以
由
，
解得
， 
，
（方法二）设
. 因为
，所以
．
由椭圆定义
可知， 
．
再由余弦定理
可得， 
．
由知， 
， 
，
【题目】2015 年 12 月，华中地区数城市空气污染指数“爆表”，此轮污染为 2015 年以来最严重的污染过程，为了探究车流量与
的浓度是否相关，现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的数据如表：
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知
与
具有线性相关关系，求
关于
的线性回归方程；（提示数据： 
）
(2)利用(1)所求的回归方程，预测该市车流量为 12 万辆时
的浓度.
参考公式：回归直线的方程是
，
其中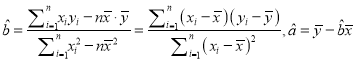
.
【题目】某水产养殖基地要将一批海鲜用汽车从所在城市甲运至销售商所在城市乙，已知从城市甲到城市乙只有两条公路，且运费由水产养殖基地承担．若水产养殖基地恰能在约定日期（×月×日）将海鲜送达，则销售商一次性支付给水产养殖基地
万元；若在约定日期前送到，每提前一天销售商将多支付给水产养殖基地
万元；若在约定日期后送到，每迟到一天销售商将少支付给水产养殖基地
万元．为保证海鲜新鲜度，汽车只能在约定日期的前两天出发，且只能选择其中的一条公路运送海鲜，已知下表内的信息：
汽车 行驶路线 | 不堵车的情况下到达城市乙所需时间（天） | 堵车的情况下到达城市乙所需时间（天） | 堵车的概率 | 运费（万元） |
公路 |
|
|
|
|
公路 |
|
|
|
|
（注：毛利润
销售商支付给水产养殖基地的费用
运费）
（Ⅰ）记汽车走公路
时水产养殖基地获得的毛利润为
（单位：万元），求
的分布列和数学期望
．
（Ⅱ）假设你是水产养殖基地的决策者，你选择哪条公路运送海鲜有可能让水产养殖基地获得的毛利润更多？
