题目内容
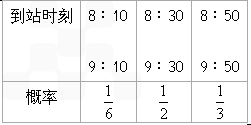
某车站每天8∶00—9∶00，9∶00—10∶00都恰有一辆客车到站，但到站的时刻是随机的，且两者到站的时间是相互独立的，其规律为
|
到站时刻 |
8∶10 9∶10 |
8∶30 9∶30 |
8∶50 9∶50 |
|
概率 |
|
|
|
一旅客8∶20到车站，则它候车时间的数学期望为 ．
【答案】
【解析】解：因为旅客乙8：20到站，他的候车时间η的取值可能为10，30，50，70，90，
P（η=10）=
P（η=30）=
，
P（η=50）=
，
P（η=70）=
，
P（η=90）=
可得分布列和期望值为
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
,
,
;9:00—10:00到站的客车可能在9:10,9:30和9:50到站,其概率依次为
,
,
.今有甲、乙两位旅客要从A地到B地,他们到达车站的时间分别是8:00和8:20,假设只要有车到站就一定能坐上车,设甲与乙的候车时间分别为ξ分钟和η分钟.
;9∶00~10∶00到站的客车B可能在9∶10，9∶30，9∶50到站，其概率依次为
.
，求
,求