题目内容
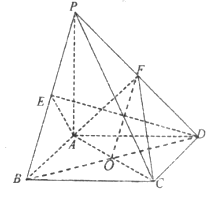
【题目】已知四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
(I)求证:PB∥平面FAC;
(II)求三棱锥P-EAD的体积;
(III)求证:平面EAD⊥平面FAC.

【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】分析:(1)连接BD,与AC交于点O,连接OF,推导出OF∥PB,由此能证明PB//平面FAC;
(2)由PA⊥平面ABCD,知![]() 为棱锥
为棱锥![]() 的高,由
的高,由![]() ,知
,知![]() ,由此能求出结果;
,由此能求出结果;
(3)推导出![]() ,从而
,从而![]() 平面
平面![]() ,进而
,进而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() .
.
详解:(I)连接BD,与AC交于点O,连接OF,
在△PBD中,O,F分别是BD,PD中点,
所以OF∥PB,
又因为OF![]() 平面FAC, PB
平面FAC, PB![]() 平面FAC,
平面FAC,
所以PB//平面FAC,
(II)法1:因为PA⊥平面ABCD,AB,AD![]() 平面ABCD,
平面ABCD,
所以PA⊥AB,PA⊥AD,
又因为AB⊥AD,![]() ,PA,AB
,PA,AB![]() 平面PAB,
平面PAB,
所以AD⊥平面PAB,
在直角△PAB中,PA=AB=2,E为PB中点,
所以![]() ,
,
所以三棱锥P-EAD的体积为![]() .
.
法2:因为PA⊥平面ABCD,所以PA为棱锥P-ABD的高.
因为PA=AB=2,底面ABCD是正方形,
所以![]() ,
,
因为E为PB中点,所以
所以![]() .
.
(III)证明:
因为AD⊥平面PAB,PB![]() 平面PAB,
平面PAB,
所以AD⊥PB,
在等腰直角△PAB中,AE⊥PB,
又![]() ,AE,AD
,AE,AD![]() 平面EAD,
平面EAD,
所以PB⊥平面EAD,
又OF∥PB,
所以OF⊥平面EAD,
又OF![]() 平面FAC,
平面FAC,
所以平面EAD⊥平面FAC.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目