题目内容

函数f（x）=是(    )

A.奇函数                                    B.偶函数

C.既是奇函数又是偶函数               D.既不是奇函数又不是偶函数

思路解析：本题考查函数奇偶性的判断原则、方法.

函数奇偶性的判断首先必须求函数的定义域，看其是否关于原点对称，然后验证f（-x）与f（x）的关系.函数f（x）=的定义域需满足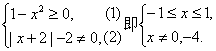

因此函数的定义域为［-1，0）∪（0，1].

此时f（x）=，f（-x）=-f（x），即函数为奇函数.

答案：A

练习册系列答案
相关题目
已知函数f（x）=2cos（2x+
π
6
），下面四个结论中正确的是（　　）
已知函数f（x）满足f（f（x））=x
（1）求出所有满足条件的一次函数f（x）
（2）函数f（x）可以是二次函数，三次函数吗？其他函数呢？
（3）研究f（x）是否具有某种对称性，若有请给出证明，若无请说明理由．
（2013•东城区模拟）若定义域为R的函数f（x）不是奇函数，则下列命题中一定为真命题的是（　　）
已知函数f（x）=x2+bx+c，且函数f（x+1）是偶函数．
（Ⅰ）求实数b的值；
（Ⅱ）若函数g（x）=|f（x）|（x∈[-1，2]）的最小值为1，求函数g（x）的最大值．
定义在R上的函数f（x）满足对于任意的α，β∈R，总有f（α+β）-f（α）-f（β）=2013．
①函数f（x）-2013是偶函数；
②函数f（x）+2013是偶函数；
③函数f（x）-2013是奇函数；
④函数f（x）+2013是奇函数．
其中说法正确的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网