题目内容
(本题14分)如图,在四棱锥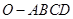 中,底面
中,底面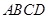 是边长为1的菱形,
是边长为1的菱形,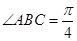 ,
, 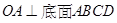 ,
, 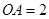 ,
,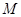 为
为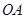 的中点,
的中点,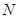 为
为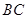 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)求异面直线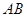 与
与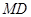 所成角的大小;
所成角的大小;
(Ⅲ)求点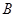 到平面
到平面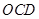 的距离.
的距离.
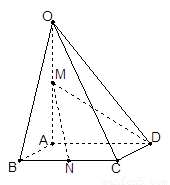
【答案】
解:如图,作 于点P, 分别以AB,AP,AO所在直线为
于点P, 分别以AB,AP,AO所在直线为
 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则
 ,
,
(1)证明:
设平面OCD的法向量为 ,则
,则
即 
取 ,解得
,解得
∵ 即
即 又∵
又∵
∴
(2)解 设 与
与 所成的角为
所成的角为 ,
,
∴  ,∵
,∵ ,∴
,∴ ,即
,即 与
与 所成角的大小为
所成角的大小为 .
.
(3)解 设点B到平面OCD的距离为 ,
,
则 为
为 在向量
在向量 上的投影的绝对值,
上的投影的绝对值,
由  , 得
, 得 ,即点B到平面OCD的距离为
,即点B到平面OCD的距离为
(综合几何方法求解略)
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,
如图,

 中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点
中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点