题目内容

函数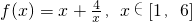 $数学公式$ ．的值域为[m，n]，则n-m=________．

$\text{[math]}$
分析：先由均值不等式求出m，再由函数的性质求出n，由此可得到n-m的结果．
解答：∵x∈[1，6]，
∴f（x）=x+ $\text{[math]}$ $\text{[math]}$ ，
所以m=4．
由题设知，n=f（6）=6+ $\text{[math]}$ = $\text{[math]}$ ．
∴ $\text{[math]}$ ．
故答案： $\text{[math]}$ ．
点评：本题考查基本不等式求最大值和最小值问题，解题时要注意均值不等式的应用条件．

练习册系列答案

中考新方向系列答案

中考新航线系列答案

专项新评价中考二轮系列答案

中考研究全国各省市中考真题常考基础题系列答案

中考通系列答案

中考添翼中考总复习系列答案

中考题库系列答案

中考升学指导系列答案

超越中考系列答案

中考全程复习训练系列答案

相关题目

设函数f(x)=ax+

(a＞0)，g（x）=4-x，已知满足f（x）=g（x）的x有且只有一个．
（Ⅰ）求a的值；
（Ⅱ）若f(x)+

＞1对一切x＞0恒成立，求m的取值范围；
（Ⅲ）若函数h（x）=k-f（x）-g（x）（k∈R）在[m，n]上的值域为[m，n]（其中n＞m＞0），求k的取值范围．

定义域为R的函数y=f（x）满足：
① $数学公式$ ；
②函数在 $数学公式$ 的值域为[m，2]，并且 $数学公式$ ，当x₁＜x₂时恒有f（x₁）＜f（x₂）．
（1）求m的值；
（2）若 $数学公式$ ，并且 $数学公式$ 求满足条件的x的集合；
（3）设y=g（x）=2cos²x+sinx+m+2，若对于y在集合M中的每一个值，x在区间（0，π）上恰有两个不同的值与之对应，求集合M．

定义域为R的函数y=f（x）满足：
①

；
②函数在

的值域为[m，2]，并且

，当x₁＜x₂时恒有f（x₁）＜f（x₂）．
（1）求m的值；
（2）若

求满足条件的x的集合；
（3）设y=g（x）=2cos²x+sinx+m+2，若对于y在集合M中的每一个值，x在区间（0，π）上恰有两个不同的值与之对应，求集合M．

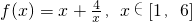．的值域为[m，n]，则n-m= ．