题目内容
如图,已知a、b是两条相互垂直的异面直线,其公垂线段AB的长为定值m,定长为n(n>m)的线段PQ的两个端点分别在a、b上移动,M、N分别是AB、PQ的中点.
(1)求证:AB⊥MN;
(2)求证:MN的长是定值.

答案:
解析:
解析:
|
(1)取PB中点H,连结HN,则HN∥b. 又∵AB⊥b∴AB⊥HN 同理AB⊥MH∴AB⊥平面MNH∴AB⊥MN (2)∵ 在Rt△PBQ中,BQ2=PQ2-PB2=n2-PB2① 在Rt△PBA中,PA2=PB2-AB2=PB2-m2② ①、②两式相加:PA2+BQ2=n2-m2 ∵a⊥b∴∠MHN= ∴MN= |

练习册系列答案
相关题目
 b⊥平面PAB,∴b⊥PB.
b⊥平面PAB,∴b⊥PB.
 =
= =
= (定值)
(定值) (2012•江苏二模)如图,已知A、B是函数y=3sin(2x+θ)的图象与x轴两相邻交点,C是图象上A,B之间的最低点,则
(2012•江苏二模)如图,已知A、B是函数y=3sin(2x+θ)的图象与x轴两相邻交点,C是图象上A,B之间的最低点,则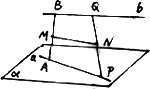
 = .
= .
 = .
= .