题目内容
函数f(x)=1-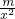 (m≠0)
(m≠0)
(1)判断函数f(x)的奇偶性.
(2)用定义判断函数f(x)在(0,+∞)上的单调性.
解:(1)函数的定义域为(-∞,0)∪(0,+∞)
∵
∴函数f(x)为偶函数;
(2)设x1>x2>0,则
∵x1>x2>0,∴
∴m>0,f(x1)-f(x2)>0;m<0,f(x1)-f(x2)<0
∴m>0,函数f(x)在(0,+∞)上单调增;m<0,函数f(x)在(0,+∞)上单调减.
分析:(1)函数的定义域为(-∞,0)∪(0,+∞),再利用 ,可判断函数f(x)为偶函数;
,可判断函数f(x)为偶函数;
(2)设x1>x2>0,则 ,对m进行讨论,可知m>0,f(x1)-f(x2)>0;m<0,f(x1)-f(x2)<0,从而可得m>0,函数f(x)在(0,+∞)上单调增;m<0,函数f(x)在(0,+∞)上单调减.
,对m进行讨论,可知m>0,f(x1)-f(x2)>0;m<0,f(x1)-f(x2)<0,从而可得m>0,函数f(x)在(0,+∞)上单调增;m<0,函数f(x)在(0,+∞)上单调减.
点评:本题以函数为载体,考查函数的奇偶性,考查函数的单调性,掌握定义是关键.
∵

∴函数f(x)为偶函数;
(2)设x1>x2>0,则

∵x1>x2>0,∴

∴m>0,f(x1)-f(x2)>0;m<0,f(x1)-f(x2)<0
∴m>0,函数f(x)在(0,+∞)上单调增;m<0,函数f(x)在(0,+∞)上单调减.
分析:(1)函数的定义域为(-∞,0)∪(0,+∞),再利用
 ,可判断函数f(x)为偶函数;
,可判断函数f(x)为偶函数;(2)设x1>x2>0,则
 ,对m进行讨论,可知m>0,f(x1)-f(x2)>0;m<0,f(x1)-f(x2)<0,从而可得m>0,函数f(x)在(0,+∞)上单调增;m<0,函数f(x)在(0,+∞)上单调减.
,对m进行讨论,可知m>0,f(x1)-f(x2)>0;m<0,f(x1)-f(x2)<0,从而可得m>0,函数f(x)在(0,+∞)上单调增;m<0,函数f(x)在(0,+∞)上单调减.点评:本题以函数为载体,考查函数的奇偶性,考查函数的单调性,掌握定义是关键.

练习册系列答案
相关题目