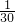Question

设x，y是0，1，2，3，4，5中任意两个不同的数，那么复数x+yi恰好是纯虚数的概率为（　　）

• A、

  1

  6

• B、

  1

  3

• C、

  1

  5

• D、

  1

  30

Answer 1

分析：本题是一个古典概型，试验发生包含的事件是从6个数字中任取2个数字，共有6×5种结果，满足条件的事件是复数x+yi恰好是纯虚数，即实部是0，这样虚部有5种结果，得到概率．

解答：解：由题意知本题是一个古典概型，
试验发生包含的事件是从6个数字中任取2个数字，共有6×5=30种结果，
满足条件的事件是复数x+yi恰好是纯虚数，即实部是0，这样虚部有5种结果，
∴复数x+yi恰好是纯虚数的概率为

5

30

=

1

6

故选A．

点评：本题考查古典概型，古典概型要求能够列举出所有事件和发生事件的个数，概率问题同其他的知识点结合在一起，实际上是以概率问题为载体，主要考查的是另一个知识点，本题主要考查复数的概念．