题目内容
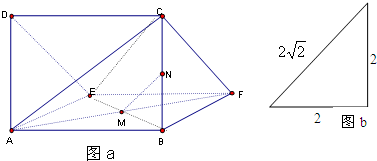 如图,一个多面体的直观图如图a所示,它的正视图和俯视图都是边长为2的正方形,左视图如图b所示.已知M、N分别是AF、BC的中点.
如图,一个多面体的直观图如图a所示,它的正视图和俯视图都是边长为2的正方形,左视图如图b所示.已知M、N分别是AF、BC的中点.(1)求证:MN∥平面CDEF;
(2)求四棱锥E-ABCD的体积.
分析:(1)由三视图可知,该多面体是底面为直角三角形的直三棱柱ADE-BCF,且AB=BC=BF=2,DE=CF=2
.∠CBF=
,由此能够证明MN∥面CDEF.
(2)由条件AB⊥AE;AD⊥AE,AD∩AB=A,从而得到AE⊥面ABCD.四棱锥E-ABCD是以AE为高,以矩形ABCD为底面的棱锥,由此能求出棱锥E-ABCD的体积.
| 2 |
| π |
| 2 |
(2)由条件AB⊥AE;AD⊥AE,AD∩AB=A,从而得到AE⊥面ABCD.四棱锥E-ABCD是以AE为高,以矩形ABCD为底面的棱锥,由此能求出棱锥E-ABCD的体积.
解答:(1)证明:由三视图可知,该多面体是底面为直角三角形的直三棱柱ADE-BCF,
且AB=BC=BF=2,DE=CF=2
.∠CBF=
,
△BEC中,MN为中位线,故MN∥CE,
又CE?面CDEF,MN?面CDEF,
∴MN∥面CDEF.
(2)解:由条件AB⊥AE,AD⊥AE,AD∩AB=A,
∴AE⊥面ABCD.
四棱锥E-ABCD是以AE为高,以矩形ABCD为底面的棱锥,
在△ADE中,AE=2,SABCD=AB•AD=4,
∴棱锥E-ABCD的体积为:V=
•SABCD•AE=
×4×2=
.
且AB=BC=BF=2,DE=CF=2
| 2 |
| π |
| 2 |
△BEC中,MN为中位线,故MN∥CE,
又CE?面CDEF,MN?面CDEF,
∴MN∥面CDEF.
(2)解:由条件AB⊥AE,AD⊥AE,AD∩AB=A,
∴AE⊥面ABCD.
四棱锥E-ABCD是以AE为高,以矩形ABCD为底面的棱锥,
在△ADE中,AE=2,SABCD=AB•AD=4,
∴棱锥E-ABCD的体积为:V=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
点评:本题考查直线与平面平行的证明,考查棱锥的体积的求法,解题时要认真审题,注意三视图的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和) 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)
 PA,求二面角D-BC-A的大小;(结果用反三角函数值表示)
PA,求二面角D-BC-A的大小;(结果用反三角函数值表示) 求二面角D-BC-A的大小;(结果用反三角函数值表示)
求二面角D-BC-A的大小;(结果用反三角函数值表示)