题目内容
已知数列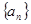 中,
中,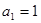 ,
,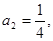 且
且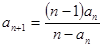
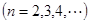 .
.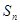 为数列
为数列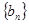 的前
的前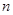 项和,且
项和,且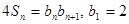
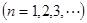 .
.
(1)求数列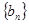 的通项公式;
的通项公式;
(2)设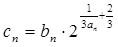 ,求数列
,求数列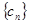 的前
的前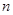 项的和
项的和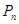 ;
;
(3)证明对一切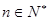 ,有
,有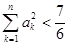 .
.
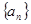 中,
中,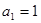 ,
,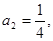 且
且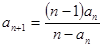
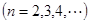 .
.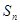 为数列
为数列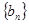 的前
的前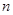 项和,且
项和,且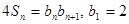
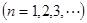 .
.(1)求数列
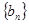 的通项公式;
的通项公式;(2)设
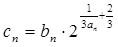 ,求数列
,求数列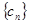 的前
的前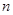 项的和
项的和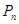 ;
;(3)证明对一切
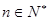 ,有
,有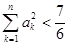 .
.(1)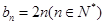 ;(2)
;(2)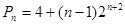 ;(3)证明过程详见解析.
;(3)证明过程详见解析.
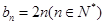 ;(2)
;(2)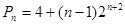 ;(3)证明过程详见解析.
;(3)证明过程详见解析.试题分析:本题主要考查数列的通项公式、递推公式、裂项相消法、数学归纳法、错位相减法等基础知识,考查学生分析问题解决问题的能力,转化能力和计算能力.第一问,用n-1代替
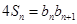 中的n,得到一个等式,2个等式相减,得到
中的n,得到一个等式,2个等式相减,得到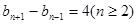 ,分n为奇数偶数进行讨论,分别求出
,分n为奇数偶数进行讨论,分别求出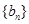 的通项公式,由于得到的式子相同,所以
的通项公式,由于得到的式子相同,所以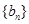 的通项公式就是
的通项公式就是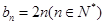 ;第二问,要求数列
;第二问,要求数列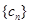 的前n项和,关键是需要求出
的前n项和,关键是需要求出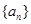 的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到
的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到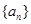 的通项公式后,代入到
的通项公式后,代入到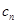 中,得到
中,得到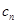 的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和
的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和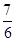 作比较.
作比较.试题解析:(1)由已知
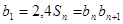 得
得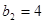 ,
, ,
,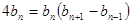 ,
,由题意
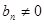 ,即
,即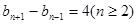 ,当n为奇数时,
,当n为奇数时,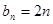 ;当n为偶数时,
;当n为偶数时,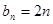 .
.所以
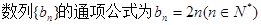 .4分
.4分(2)解法一:由已知,对
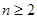 有
有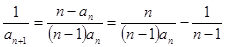 ,
,两边同除以
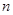 ,得
,得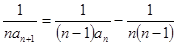 ,即
,即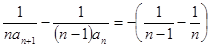 ,
,于是,
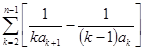 =
=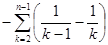 =
=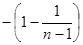 ,
,即
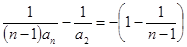 ,
,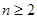 ,所以
,所以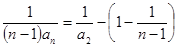 =
=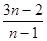 ,
,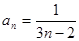 ,
,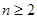 ,又
,又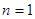 时也成立,故
时也成立,故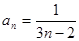 ,
,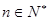 .
.所以
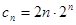 ,
,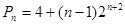 8分
8分解法二:也可以归纳、猜想得出
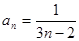 ,然后用数学归纳法证明.
,然后用数学归纳法证明.(3)当
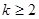 ,有
,有 ,
,所以
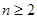 时,有
时,有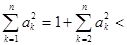
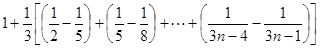
=
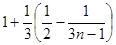
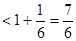 .
.当
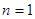 时,
时,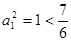 .故对一切
.故对一切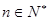 ,有
,有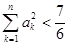 .14分
.14分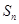 求
求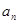 ;2.错位相减法;3.数学归纳法;4.裂项相消法.
;2.错位相减法;3.数学归纳法;4.裂项相消法.
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
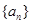 中,
中,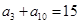 ,且
,且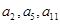 成等比数列.
成等比数列.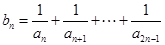 ,证明:
,证明: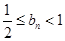 .
.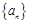 的前n项和为Sn,已知
的前n项和为Sn,已知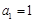 ,且
,且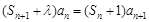 对一切
对一切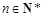 都成立.
都成立.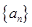 是首项为
是首项为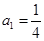 ,公比
,公比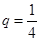 的等比数列,设
的等比数列,设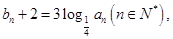 .
.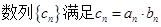
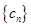 的前n项和
的前n项和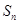 ;
;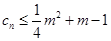 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.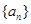 是公比大于
是公比大于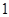 的等比数列,
的等比数列,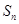 为数列
为数列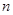 项和.已知
项和.已知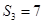 ,且
,且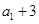 ,
,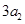 ,
,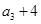 构成等差数列.
构成等差数列.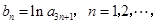 求数列
求数列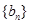 的前
的前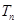 .
. 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 中最大的是()
中最大的是()



 表示数列
表示数列 的前
的前 项的和,若对任意
项的和,若对任意 满足
满足 且
且
 =( )
=( )



 的通项公式为
的通项公式为 ,数列
,数列 的通项公式为
的通项公式为 ,
, 若在数列
若在数列 中,
中, 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .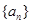 ,若点
,若点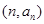
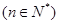 均在直线
均在直线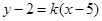 上,则数列
上,则数列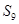 等于( )
等于( )