题目内容
设函数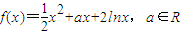 ,已知f(x)在x=1处有极值.
,已知f(x)在x=1处有极值.(1)求实数a的值;
(2)当
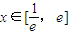 (其中e是自然对数的底数)时,证明:e(e-x)(e+x-6)+4≥x4;
(其中e是自然对数的底数)时,证明:e(e-x)(e+x-6)+4≥x4;(3)证明:对任意的n>1,n∈N*,不等式
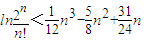 恒成立.
恒成立.
【答案】分析:(1)由题意函数 ,已知f(x)在x=1处有极值,所以f′(1)=0,进而建立a的方程,解出即可;
,已知f(x)在x=1处有极值,所以f′(1)=0,进而建立a的方程,解出即可;
(2)由题意对函数求导,求出函数的单调区间及函数的单调性,即可证明;
(3)有(2)可知函数在定义域上的最大值,利用累加法即可得证.
解答:解:(1)由题意函数 ,已知f(x)在x=1处有极值,
,已知f(x)在x=1处有极值,
所以f′(1)=0∴1+a+2=0解得:a=-3.
(2)∵ ,(x>0)
,(x>0)
∴ ,
,
由 ,
,
 ,
,
∵ ∴函数f(x)的单调递增区间为(
∴函数f(x)的单调递增区间为( .(2,e),单调的减区间为(1,2),
.(2,e),单调的减区间为(1,2),
∴ =
= ,又f(e)=
,又f(e)= ,
,
f(e)-f(1)=
∴ e2-3e+2
e2-3e+2
∴
即:e2-6e+4≥x2-6x+4lnx
即:e2-x2+6x-6e+4≥4lnx⇒(e-x)(e+x-6)+4≥4lnx
∴
∴e(e-x)(e+x-6)+4≥x4;
(3)∵ ,函数f(x)的单调递减区间为(1,2),单调递增区间为(2,e),
,函数f(x)的单调递减区间为(1,2),单调递增区间为(2,e),
∴当x∈(1,+∞)时,函数f(x)在x=2处取得最小值2ln2-4,
∴

∴ ,
,
∵

…

由于以上各式并不都能取等号,所以把以上各式相加,变形得:




 =
=
∴
 .
.
点评:此题考查了函数极值的定义,还考查了利用导函数判断函数在定义域上的单调性及最值,还有利用累加法证明与n有关的命题.
 ,已知f(x)在x=1处有极值,所以f′(1)=0,进而建立a的方程,解出即可;
,已知f(x)在x=1处有极值,所以f′(1)=0,进而建立a的方程,解出即可;(2)由题意对函数求导,求出函数的单调区间及函数的单调性,即可证明;
(3)有(2)可知函数在定义域上的最大值,利用累加法即可得证.
解答:解:(1)由题意函数
 ,已知f(x)在x=1处有极值,
,已知f(x)在x=1处有极值,所以f′(1)=0∴1+a+2=0解得:a=-3.
(2)∵
 ,(x>0)
,(x>0)∴
 ,
,由
 ,
, ,
,∵
 ∴函数f(x)的单调递增区间为(
∴函数f(x)的单调递增区间为( .(2,e),单调的减区间为(1,2),
.(2,e),单调的减区间为(1,2),∴
 =
= ,又f(e)=
,又f(e)= ,
,f(e)-f(1)=

∴
 e2-3e+2
e2-3e+2∴

即:e2-6e+4≥x2-6x+4lnx
即:e2-x2+6x-6e+4≥4lnx⇒(e-x)(e+x-6)+4≥4lnx
∴

∴e(e-x)(e+x-6)+4≥x4;
(3)∵
 ,函数f(x)的单调递减区间为(1,2),单调递增区间为(2,e),
,函数f(x)的单调递减区间为(1,2),单调递增区间为(2,e),∴当x∈(1,+∞)时,函数f(x)在x=2处取得最小值2ln2-4,
∴


∴
 ,
,∵


…

由于以上各式并不都能取等号,所以把以上各式相加,变形得:




 =
=
∴

 .
.点评:此题考查了函数极值的定义,还考查了利用导函数判断函数在定义域上的单调性及最值,还有利用累加法证明与n有关的命题.

练习册系列答案
相关题目
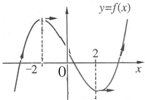 设f′(x)是函数f(x)的导函数,已知f(x)在R上的图象(如图),若f′(x)>0,则x的取值范围是
设f′(x)是函数f(x)的导函数,已知f(x)在R上的图象(如图),若f′(x)>0,则x的取值范围是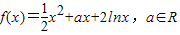 ,已知f(x)在x=1处有极值.
,已知f(x)在x=1处有极值.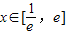 (其中e是自然对数的底数)时,证明:e(e-x)(e+x-6)+4≥x4;
(其中e是自然对数的底数)时,证明:e(e-x)(e+x-6)+4≥x4;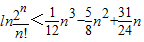 恒成立.
恒成立.