题目内容

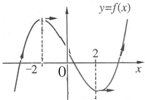设f′（x）是函数f（x）的导函数，已知f（x）在R上的图象（如图），若f′（x）＞0，则x的取值范围是
（-∞，-2）∪（2，+∞）
（-∞，-2）∪（2，+∞）
．
分析：利用导数与函数单调性的关系即可得出．
解答：解：由图可知：当x＜-2，或x＞2时，函数f（x）单调递增，则f′（x）＞0．
故答案为（-∞，-2）∪（2，+∞）．
点评：熟练掌握导数与函数单调性的关系设解题的关键．
练习册系列答案
相关题目
12、设f′（x）是函数f（x）的导函数，有下列命题：
①存在函数f（x），使函数y=f（x）-f′（x）为偶函数；
②存在函数f（x）f′（x）≠0，使y=f（x）与y=f′（x）的图象相同；
③存在函数f（x）f′（x）≠0使得y=f（x）与y=f′（x）的图象关于x轴对称．
其中真命题的个数为（　　）
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）
设f′（x）是函数f（x）的导函数，有下列命题：
①存在函数f（x），使函数y=f（x）-f′（x）为偶函数；
②存在函数f（x）f′（x）≠0，使y=f（x）与y=f′（x）的图象相同；
③存在函数f（x）f′（x）≠0使得y=f（x）与y=f′（x）的图象关于x轴对称．
其中真命题的个数为（ ）
A．0
B．1
C．2
D．3
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网