题目内容
已知椭圆
解法一:设弦MN所在的直线方程为y-1=k(x-2),
代入椭圆的方程并整理,得(9+16k2)x2-32k(2k-1)x+64(k2-k-2)=0.
设M(x1,y1)、N(x2,y2),
由韦达定理可得x1+x2=![]() . ①
. ①
∵P(2,1)是MN的中点,
∴![]() =2,即x1+x2=4. ②
=2,即x1+x2=4. ②
由①②可得![]() =4,解得k=-
=4,解得k=-![]() .
.
故弦MN所在的直线方程是y-1=-![]() (x-2),
(x-2),
即为9x+8y-26=0.
解法二:设弦MN的两端点的坐标为M(x1,y1)、N(x2,y2),直线MN的斜率为k,则
9x12+16y12=144, ③
9x22+16y22=144, ④
③-④,得9(x1+x2)(x1-x2)+16(y1+y2)(y1-y2)=0. ⑤
∵P(2,1)是MN的中点,
∴x1+x2=4,y1+y2=2,代入⑤得k=![]() =-
=-![]() .
.
故直线MN的方程为y-1=-![]() (x-2),即9x+8y-26=0.
(x-2),即9x+8y-26=0.

练习册系列答案
相关题目
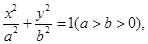 以双曲线
以双曲线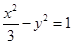 的焦点为顶点,其离心率与双曲线的离心率互为倒数.
的焦点为顶点,其离心率与双曲线的离心率互为倒数. ,
, ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
. 、
、 ,证明
,证明 ;
; ,使得
,使得

 ,求以点P(2,-1)为中点的弦AB所在的直线方程.
,求以点P(2,-1)为中点的弦AB所在的直线方程. ,求以点P(2,-1)为中点的弦AB所在的直线方程.
,求以点P(2,-1)为中点的弦AB所在的直线方程.