题目内容
如图,简单组合体ABCDPE,其底面ABCD为边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.(1)若N为线段PB的中点,求证:EN∥平面ABCD;
(2)求点D到平面PBE的距离.
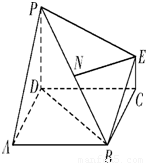
【答案】分析:解法1(几何法):(1)连接AC与BD交于点F,连接NF,根据中位线定理及平行四边形判定定理和性质,可得NE∥FC,进而由线面平行的判定定理得到EN∥平面ABCD
(2)连接DE,可得BC是三棱锥B-PDE的高,利用等积法,根据棱锥D-PBE与棱锥B-PDE是同一棱锥,体积相等,可求出点D到平面PBE的距离
解法2(向量法):(1)以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系,根据直线EN的方向向量与平面ABCD的法向量垂直,可证得EN∥平面ABCD;
(2)求出平面PBE的法向量为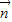 ,根据点D到平面PBE的距离
,根据点D到平面PBE的距离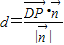 ,可得点D到平面PBE的距离
,可得点D到平面PBE的距离
解答:解:(1)解法1(几何法):
连接AC与BD交于点F,连接NF,…..(1分)
∵F为BD的中点,
∴NF∥PD且NF= PD….3分
PD….3分
又EC∥PD,且EC= PD,
PD,
∴NF∥EC,且NF=EC,
∴四边形NFCE为平行四边形,….…4分
∴NE∥FC.….….….….5分
∵NE?平面ABCD,且FC?平面ABCD
所以EN∥平面ABCD;….6分
(2)连接DE,由题PD⊥BC,且DC⊥BC,故BC是三棱锥B-PDE的高,
在直角梯形PDCE中,可求得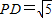 ,且
,且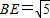 由(1)所以EN⊥PB…9分
由(1)所以EN⊥PB…9分
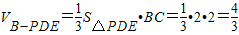 ,….….…11分
,….….…11分
又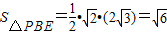 ,….….…12分
,….….…12分
设所求的距离为d,则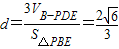 ….….…..14分
….….…..14分
解法2(向量法):
(1)以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图所示:….…1分,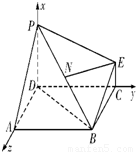
则B(2,2,0),C(0,2,0),P(0,0,2),E(0,2,1),N(1,1,1),….….….…2分
∴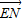 =(1,-1,0),
=(1,-1,0),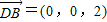 …..3分
…..3分
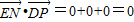
∴EN⊥PD,….….…4分
又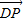 是平面ABCD的法向量
是平面ABCD的法向量
∵NE?平面ABCD
所以EN∥平面ABCD;….6分
(2)由(1)可知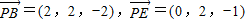 ,….8分
,….8分
设平面PBE的法向量为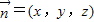
由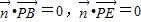 得
得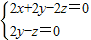 ….…10分
….…10分
解得其中一个法向量为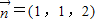 …..11分
…..11分
点D到平面PBE的距离为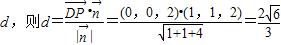 …14分
…14分
点评:本题考查的知识点是用空间向量求点到面的距离,直线与平面平行的判定,几何法证明要掌握掌握空间线面关系的判定定理及性质定理,向量法证明关键是建立空间坐标系,将空间线面夹角转化为向量夹角,将空间点面距离转化为向量的投影.
(2)连接DE,可得BC是三棱锥B-PDE的高,利用等积法,根据棱锥D-PBE与棱锥B-PDE是同一棱锥,体积相等,可求出点D到平面PBE的距离
解法2(向量法):(1)以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系,根据直线EN的方向向量与平面ABCD的法向量垂直,可证得EN∥平面ABCD;
(2)求出平面PBE的法向量为
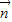 ,根据点D到平面PBE的距离
,根据点D到平面PBE的距离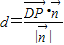 ,可得点D到平面PBE的距离
,可得点D到平面PBE的距离解答:解:(1)解法1(几何法):
连接AC与BD交于点F,连接NF,…..(1分)
∵F为BD的中点,
∴NF∥PD且NF=
 PD….3分
PD….3分又EC∥PD,且EC=
 PD,
PD,∴NF∥EC,且NF=EC,
∴四边形NFCE为平行四边形,….…4分
∴NE∥FC.….….….….5分
∵NE?平面ABCD,且FC?平面ABCD
所以EN∥平面ABCD;….6分
(2)连接DE,由题PD⊥BC,且DC⊥BC,故BC是三棱锥B-PDE的高,
在直角梯形PDCE中,可求得
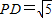 ,且
,且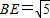 由(1)所以EN⊥PB…9分
由(1)所以EN⊥PB…9分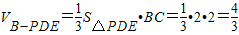 ,….….…11分
,….….…11分又
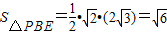 ,….….…12分
,….….…12分设所求的距离为d,则
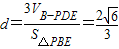 ….….…..14分
….….…..14分解法2(向量法):
(1)以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图所示:….…1分,

则B(2,2,0),C(0,2,0),P(0,0,2),E(0,2,1),N(1,1,1),….….….…2分
∴
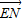 =(1,-1,0),
=(1,-1,0),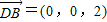 …..3分
…..3分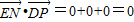
∴EN⊥PD,….….…4分
又
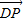 是平面ABCD的法向量
是平面ABCD的法向量∵NE?平面ABCD
所以EN∥平面ABCD;….6分
(2)由(1)可知
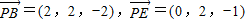 ,….8分
,….8分设平面PBE的法向量为
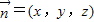
由
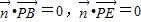 得
得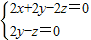 ….…10分
….…10分解得其中一个法向量为
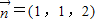 …..11分
…..11分点D到平面PBE的距离为
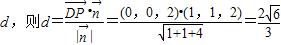 …14分
…14分点评:本题考查的知识点是用空间向量求点到面的距离,直线与平面平行的判定,几何法证明要掌握掌握空间线面关系的判定定理及性质定理,向量法证明关键是建立空间坐标系,将空间线面夹角转化为向量夹角,将空间点面距离转化为向量的投影.

练习册系列答案
相关题目
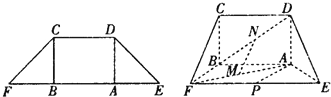 如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2
如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2


 如图(1)为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图(1)为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.