题目内容
已知双曲线的方程为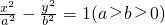 ,它的一个顶点到一条渐近线的距离为
,它的一个顶点到一条渐近线的距离为 (c为双曲线的半焦距长),则双曲线的离心率为
(c为双曲线的半焦距长),则双曲线的离心率为
- A.

- B.

- C.

- D.

B
分析:不妨设它的一个顶点(a,0)到一条渐近线y= 的距离为
的距离为 ,由此利用点到直线的距离建立方程,根据a>b,即可确定双曲线的离心率.
,由此利用点到直线的距离建立方程,根据a>b,即可确定双曲线的离心率.
解答:不妨设它的一个顶点(a,0)到一条渐近线y= 的距离为
的距离为 ,
,
则
∴
∴2e4-9e2+9=0
∴e2=3或
∵a>b,∴2a2>c2
∴e2<2
∴
∴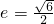
故选B.
点评:本题重点考查双曲线的几何性质,考查点到直线距离公式的运用,根据一个顶点到一条渐近线的距离为 ,建立方程是解题的关键.
,建立方程是解题的关键.
分析:不妨设它的一个顶点(a,0)到一条渐近线y=
 的距离为
的距离为 ,由此利用点到直线的距离建立方程,根据a>b,即可确定双曲线的离心率.
,由此利用点到直线的距离建立方程,根据a>b,即可确定双曲线的离心率.解答:不妨设它的一个顶点(a,0)到一条渐近线y=
 的距离为
的距离为 ,
,则

∴

∴2e4-9e2+9=0
∴e2=3或

∵a>b,∴2a2>c2
∴e2<2
∴

∴
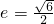
故选B.
点评:本题重点考查双曲线的几何性质,考查点到直线距离公式的运用,根据一个顶点到一条渐近线的距离为
 ,建立方程是解题的关键.
,建立方程是解题的关键. 
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目