Question

在△ABC中，内角A，B，C的对边分别为a，b，c，已知C=2A，cosA=，b=5，则△ABC的面积为________．

Answer 1

分析：由题意可求得sin2A，sin3A，再利用正弦定理==可求得c，从而可求得△ABC的面积．
解答：解；∵在△ABC中，C=2A，
∴B=π-A-C=π-3A，
又cos A=，
∴sinA=，sin2A=2sinAcosA=，
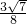sinB=sin（π-3A）=sin3A=3sinA-4sin³A，又b=5，
∴由正弦定理=得：=，
∴c=====6，
∴S_△ABC=bcsinA
=×5×6×
=．
故答案为：
点评：本题考查正弦定理，考查二倍角的正弦与三倍角的正弦公式，考查转化分析与运算能力，属于中档题．