题目内容
19.对于正实数a,函数y=x+$\frac{a}{x}$在($\frac{3}{4}$,+∞)上为增函数,则a的取值范围为 ( )| A. | ($\frac{2}{3}$,+∞) | B. | (0,$\frac{9}{16}$] | C. | (0.+∞) | D. | ($\frac{9}{16}$,+∞) |
分析 若函数y=x+$\frac{a}{x}$在($\frac{3}{4}$,+∞)上为增函数,则y′=1-$\frac{a}{{x}^{2}}$≥0在($\frac{3}{4}$,+∞)上恒成立,进而得到a的取值范围.
解答 解:∵函数y=x+$\frac{a}{x}$在($\frac{3}{4}$,+∞)上为增函数,
∴y′=1-$\frac{a}{{x}^{2}}$≥0在($\frac{3}{4}$,+∞)上恒成立,
即a≤$\frac{9}{16}$,
即正实数a的取值范围为 (0,$\frac{9}{16}$],
故选:B.
点评 本题考查的知识点是函数的单调性,导数符号与函数单调性的关系,难度中档.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
7.已知f(x)是定义在R上且以4为周期的奇函数,当x∈(0,2)时,$f(x)={2^{|x-1|}}-\frac{3}{2}$,则函数f(x)在区间[0,8]上的所有零点的和为( )
| A. | 16 | B. | 32 | C. | 48 | D. | 52 |
14.函数y=f(x)在[-2,2]上的图象如图所示,则此函数的最小值、最大值分别是( )
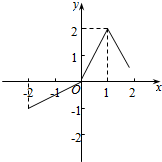
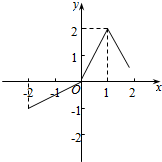
| A. | f(-2),0 | B. | 0,2 | C. | f(-2),2 | D. | f(2),2 |