题目内容
已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线![]() 相切,
相切,![]() 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点, ![]() 为椭圆
为椭圆![]() 上的动点.
上的动点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若![]() 与
与![]() 均不重合,设直线
均不重合,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(Ⅲ)![]() 为过
为过![]() 且垂直于
且垂直于![]() 轴的直线上的点,若
轴的直线上的点,若![]() ,求点
,求点![]() 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
解析:(Ⅰ)由题意可得圆的方程为![]() ,
,
∵直线![]() 与圆相切,∴
与圆相切,∴![]() ,即
,即![]() ,----------------1分
,----------------1分
又![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以椭圆方程为![]() .---------------------------------------3分
.---------------------------------------3分
![]() (Ⅱ)设
(Ⅱ)设![]() ,
, ![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,
,
则![]() ,
,![]() , --------------------------------------4分
, --------------------------------------4分
即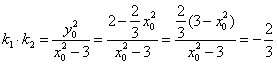 ,
,
∴![]() 为定值
为定值![]() .-------------------------------6分
.-------------------------------6分
(Ⅲ)设![]() ,其中
,其中![]() .
.
由已知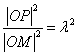 及点
及点![]() 在椭圆
在椭圆![]() 上可得
上可得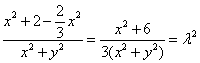 ,
,
整理得![]() ,其中
,其中![]() .-------------------------7分
.-------------------------7分
①当![]() 时,化简得
时,化简得![]() ,
,
所以点![]() 的轨迹方程为
的轨迹方程为![]() ,轨迹是两条平行于
,轨迹是两条平行于![]() 轴的线段;
轴的线段;
------------------8分
②当![]() 时,方程变形为
时,方程变形为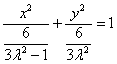 ,其中
,其中![]() ,
,
------------------------------------10分
当![]() 时,点
时,点![]() 的轨迹为中心在原点、实轴在
的轨迹为中心在原点、实轴在![]() 轴上的双曲线满足
轴上的双曲线满足![]() 的部分;
的部分;
当![]() 时,点
时,点![]() 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在![]() 轴上的椭圆满足
轴上的椭圆满足![]() 的部分;
的部分;
当![]() 时,点
时,点![]() 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在![]() 轴上的椭圆. ---------------------------------------12分
轴上的椭圆. ---------------------------------------12分

练习册系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: