Question

【题目】已知抛物线，其焦点为.

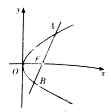
（1）若点，求以为中点的抛物线的弦所在的直线方程；

（2）若互相垂直的直线都经过抛物线的焦点，且与抛物线相交于两点和两点，求四边形面积的最小值.

Answer 1

【答案】（1）；（2）.

【解析】

试题分析：（1）用点差法求中点弦所在的直线方程；（2）利用抛物线的定义求抛物线的焦点弦长，表示四边形的面积，再利用均值不等式求面积的最值.

试题解析：（1）因为点抛物线含焦点的区域内，所以中点弦所在的直线存在.设所求直线交拋物线于,,则,, 所求直线方程为: .

依题意知，直线的斜率存在，设直线的方程为,与抛物线方程联立，得

,消，整理得，其两根为, 且.

由抛物线的定义可知, , 同理,所以四边形的面积.当且仅当时取得最小值.