题目内容
求函数f(x)=x2-4x+(2-a)lnx(a∈R)在区间[e,e2]上的最小值.
解:当x∈[e,e2]时,f(x)=x2-4x+(2-a)lnx,
所以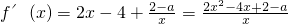 ,
,
设g(x)=2x2-4x+2-a.
①当a≤0时,有△=16-4×2(2-a)=8a≤0
所以f'(x)≥0,f(x)在[e,e2]上单调递增.
所以f(x)min=f(e)=e2-4e+2-a
②当a>0时,△=16-4×2(2-a)=8a>0,
令f'(x)>0,即2x2-4x+2-a>0,解得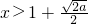 或
或 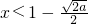 (舍);
(舍);
令f'(x)<0,即2x2-4x+2-a<0,解得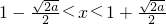 .
.
10若 ,即a≥2(e2-1)2时,f(x)在区间[e,e2]单调递减,
,即a≥2(e2-1)2时,f(x)在区间[e,e2]单调递减,
所以f(x)min=f(e2)=e4-4e2+4-2a.
20若 ,即2(e-1)2<a<2(e2-1)2时,f(x)在区间
,即2(e-1)2<a<2(e2-1)2时,f(x)在区间 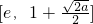 上单调递减,
上单调递减,
在区间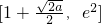 上单调递增,所以
上单调递增,所以 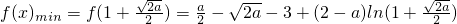 .
.
30若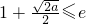 ,即0<a≤2(e-1)2时,f(x)在区间[e,e2]单调递增,
,即0<a≤2(e-1)2时,f(x)在区间[e,e2]单调递增,
所以f(x)min=f(e)=e2-4e+2-a.
综上所述,
当a≥2(e2-1)2时,f(x)min=e4-4e2+4-2a;
当2(e-1)2<a<2(e2-1)2时, ;
;
当a≤2(e-1)2时,f(x)min=e2-4e+2-a.
分析:先求函数的导数,即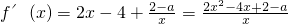 ,再令g(x)=2x2-4x+2-a,对a进行讨论,从而得到
,再令g(x)=2x2-4x+2-a,对a进行讨论,从而得到
f′(x)的符号,进而得到f(x)的单调性,从而得到函数的极值点、端点的函数值,比较极小值与端点函数值的大小,近而求出最小值.
点评:本题考查了复合函数的在闭区间上的最值问题,还有分类讨论的思想,属于中档题.
所以
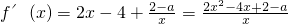 ,
,设g(x)=2x2-4x+2-a.
①当a≤0时,有△=16-4×2(2-a)=8a≤0
所以f'(x)≥0,f(x)在[e,e2]上单调递增.
所以f(x)min=f(e)=e2-4e+2-a
②当a>0时,△=16-4×2(2-a)=8a>0,
令f'(x)>0,即2x2-4x+2-a>0,解得
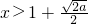 或
或 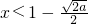 (舍);
(舍);令f'(x)<0,即2x2-4x+2-a<0,解得
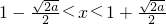 .
.10若
 ,即a≥2(e2-1)2时,f(x)在区间[e,e2]单调递减,
,即a≥2(e2-1)2时,f(x)在区间[e,e2]单调递减,所以f(x)min=f(e2)=e4-4e2+4-2a.
20若
 ,即2(e-1)2<a<2(e2-1)2时,f(x)在区间
,即2(e-1)2<a<2(e2-1)2时,f(x)在区间 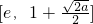 上单调递减,
上单调递减,在区间
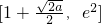 上单调递增,所以
上单调递增,所以 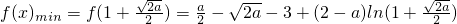 .
.30若
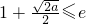 ,即0<a≤2(e-1)2时,f(x)在区间[e,e2]单调递增,
,即0<a≤2(e-1)2时,f(x)在区间[e,e2]单调递增,所以f(x)min=f(e)=e2-4e+2-a.
综上所述,
当a≥2(e2-1)2时,f(x)min=e4-4e2+4-2a;
当2(e-1)2<a<2(e2-1)2时,
 ;
;当a≤2(e-1)2时,f(x)min=e2-4e+2-a.
分析:先求函数的导数,即
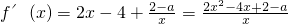 ,再令g(x)=2x2-4x+2-a,对a进行讨论,从而得到
,再令g(x)=2x2-4x+2-a,对a进行讨论,从而得到f′(x)的符号,进而得到f(x)的单调性,从而得到函数的极值点、端点的函数值,比较极小值与端点函数值的大小,近而求出最小值.
点评:本题考查了复合函数的在闭区间上的最值问题,还有分类讨论的思想,属于中档题.

练习册系列答案
相关题目
要解决下面四个问题,只用顺序结构画不出其程序框图的是( )
A、利用1+2+…+n=
| ||
| B、当图面积已知时,求圆的周长 | ||
| C、当给定一个数x,求其绝对值 | ||
| D、求函数f(x)=x2-4x+5的函数值 |