题目内容
是否同时存在满足下列条件的双曲线,若存在,求出其方程,若不存在,说明理由.
(1)焦点在 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为 ;
;
(2)点 到双曲线上动点
到双曲线上动点 的距离最小值为
的距离最小值为 .
.
存在双曲线的方程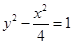 满足题中的两个条件.
满足题中的两个条件.
解析试题分析:先根据(1)的条件设出双曲线的方程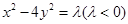 ,再设双曲线上的动点
,再设双曲线上的动点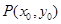 ,然后利用两点间的距离公式得出
,然后利用两点间的距离公式得出 ,结合
,结合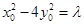 ,最后化简得到
,最后化简得到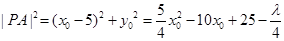 ,根据二次函数的图像与性质确定
,根据二次函数的图像与性质确定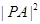 的最小值(含
的最小值(含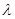 ),并由
),并由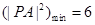 计算出
计算出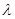 的值,如果
的值,如果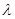 有解并满足
有解并满足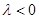 即可写出双曲线的方程;如果
即可写出双曲线的方程;如果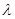 无解,则不存在满足要求的双曲线方程.
无解,则不存在满足要求的双曲线方程.
试题解析:由(1)知,设双曲线为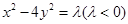
设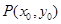 在双曲线上,由双曲线焦点在
在双曲线上,由双曲线焦点在 轴上,
轴上,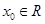 ,
,
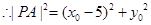
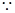
 在双曲线上
在双曲线上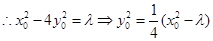
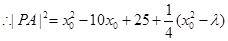
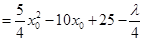
关于 的二次函数的对称轴为
的二次函数的对称轴为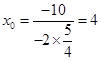
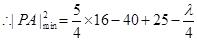
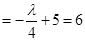
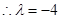
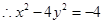 即
即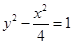
所以存在双曲线的方程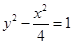 满足题中的两个条件.
满足题中的两个条件.
考点:1.双曲线的标准方程及其几何性质;2.二次函数的图像与性质.

练习册系列答案
相关题目
 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N. 时,求k的值.
时,求k的值. .
. 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率 ,直线
,直线 交椭圆于M,N两点。
交椭圆于M,N两点。 ,求弦MN的长;
,求弦MN的长;
 的最大值
的最大值 ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .
. ,求圆P的方程.
,求圆P的方程. 过点P(1,
过点P(1, 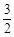 ),其左、右焦点分别为F1,F2,离心率e=
),其左、右焦点分别为F1,F2,离心率e= , M, N是直线x=4上的两个动点,且
, M, N是直线x=4上的两个动点,且 ·
· =0.
=0.
 =1的焦距为2,求椭圆上的一点到两个焦点的距离之和.
=1的焦距为2,求椭圆上的一点到两个焦点的距离之和. ·
· =1.设|
=1.设| c.若以O为中心,F为一个焦点的椭圆经过点Q,当|
c.若以O为中心,F为一个焦点的椭圆经过点Q,当|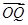 |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.