题目内容
如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船,
(Ⅰ)求接到救援命令时救援船距渔船的距离;
(Ⅱ)试问救援船在C处应朝北偏东多少度的方向沿直线前往B处救援?
(已知cos49°= )
)
(Ⅰ)求接到救援命令时救援船距渔船的距离;
(Ⅱ)试问救援船在C处应朝北偏东多少度的方向沿直线前往B处救援?
(已知cos49°=
 )
) 
解:(Ⅰ)由题意,得△ABC中,AB=20,AC=10,∠CAB=120°,
∴CB2=AB2+AC2-2AB·ACcos∠CAB,
即CB2=202+102-2×20×10cos120°=700, ,
,
所以接到救援命令时救援船距渔船的距离为 海里。
海里。
(Ⅱ)△ABC中,AB=20, ,∠CAB=120°,
,∠CAB=120°,
由正弦定理,得 ,即
,即 ,
,
∴ ,
,
 ,
,
∴∠ACB=41°,
故救援船应沿北偏东71°的方向救援。
∴CB2=AB2+AC2-2AB·ACcos∠CAB,
即CB2=202+102-2×20×10cos120°=700,
 ,
,所以接到救援命令时救援船距渔船的距离为
 海里。
海里。(Ⅱ)△ABC中,AB=20,
 ,∠CAB=120°,
,∠CAB=120°,由正弦定理,得
 ,即
,即 ,
,∴
 ,
, ,
,∴∠ACB=41°,
故救援船应沿北偏东71°的方向救援。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
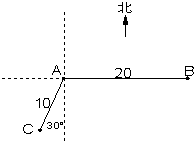 如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.
如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船. )
) 
 ).
).
 ).
).