题目内容
19.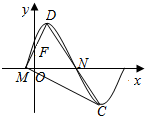 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M、N是它与x轴的两个交点,D、C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,$\overrightarrow{MD}$•$\overrightarrow{MN}$=$\frac{{π}^{2}}{18}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M、N是它与x轴的两个交点,D、C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,$\overrightarrow{MD}$•$\overrightarrow{MN}$=$\frac{{π}^{2}}{18}$.(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间.
分析 (1)由图象以及函数f(x)的解析式可以得出M,N,D三点的坐标:$M(-\frac{φ}{ω},0)$,$N(\frac{π}{ω}-\frac{φ}{ω},0)$,$D(\frac{π}{2ω}-\frac{φ}{ω},A)$,而根据条件MD的中点为F(0,1)及$\overrightarrow{MD}•\overrightarrow{MN}=\frac{{π}^{2}}{18}$即可建立关于A,ω,φ三个参数的值,从而得出f(x)=$2sin(3x+\frac{π}{4})$;
(2)根据正弦函数的单调递增区间,可令$-\frac{π}{2}+2kπ≤3x+\frac{π}{4}≤\frac{π}{2}+2kπ$,k∈Z,解出x的范围即可得出该函数的单调递增区间.
解答 解:(1)根据f(x)的解析式及图象可得以下几点坐标:
$M(-\frac{φ}{ω},0)$,$N(\frac{π}{ω}-\frac{φ}{ω},0)$,$D(\frac{π}{2ω}-\frac{φ}{ω},A)$;
∴$\overrightarrow{MN}=(\frac{π}{ω},0),\overrightarrow{MD}=(\frac{π}{2ω},A)$;
∵MD的中点为F(0,1),$\overrightarrow{MD}•\overrightarrow{MN}=\frac{{π}^{2}}{18}$;
∴$\left\{\begin{array}{l}{\frac{\frac{π}{2ω}-\frac{2φ}{ω}}{2}=0}\\{\frac{A+0}{2}=1}\\{\frac{π}{ω}•\frac{π}{2ω}+0=\frac{{π}^{2}}{18}}\end{array}\right.$;
解得$φ=\frac{π}{4},A=2,ω=3$;
∴$f(x)=2sin(3x+\frac{π}{4})$;
(2)令$-\frac{π}{2}+2kπ≤3x+\frac{π}{4}≤\frac{π}{2}+2kπ$,k∈Z;
∴$-\frac{π}{4}+\frac{2kπ}{3}≤x≤\frac{π}{12}+\frac{2kπ}{3}$,k∈Z;
∴函数f(x)的单调递增区间为$[-\frac{π}{4}+\frac{2kπ}{3},\frac{π}{12}+\frac{2kπ}{3}]$,k∈Z.
点评 考查形如y=Asin(ωx+φ)的函数的周期、最高点,图象的平移变换,根据函数解析式f(x)=Asin(ωx+φ)和图象可以确定图象的最高点,以及和x轴交点的坐标,中点坐标公式,以及向量数量积的坐标运算,以及形如y=Asin(ωx+φ)的函数的单调区间的求法.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是真命题 | D. | 命题p∨(?q)是假命题 |