题目内容
15.在直三棱柱A1B1C1-ABC中,$∠BAC=\frac{π}{2}$,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为( )| A. | [$\frac{\sqrt{5}}{5}$,1) | B. | [$\frac{\sqrt{5}}{5}$,1] | C. | ($\frac{2\sqrt{5}}{5}$,1) | D. | [$\frac{2\sqrt{5}}{5}$,1) |
分析 根据直三棱柱中三条棱两两垂直,本题考虑利用空间坐标系解决.建立如图所示的空间直角坐标系,设出F、D的坐标,利用GD⊥EF求得关系式,写出DF的表达式,然后利用二次函数求最值即可.
解答 解:建立如图所示的空间直角坐标系,则A(0,0,0),E(0,1,$\frac{1}{2}$),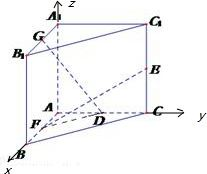
G($\frac{1}{2}$,0,1),F(x,0,0),D(0,y,0)
由于GD⊥EF,所以x+2y-1=0
DF=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{5(y-\frac{2}{5})^{2}+\frac{1}{5}}$
当y=$\frac{2}{5}$时,线段DF长度的最小值是$\frac{1}{\sqrt{5}}$
当y=1时,线段DF长度的最大值是 1
而不包括端点,故y=1不能取;
故选:A.
点评 本小题主要考查点、线、面间的距离计算、棱柱的结构特征、空间直角坐标系等基础知识,考查运算求解能力,考查空间想象能力.属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
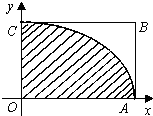 如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01)
如图,曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1(0≤x≤3,0≤y≤2),为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积,现采用随机模拟方式产生x∈(0,3),y∈(0,2)的200个点(x,y),经统计,落在图中阴影部分的点共157个,则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84.(精确到0.01)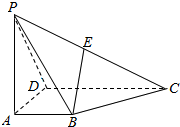 如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.
如图所示,四棱锥P-ABCD的底面是一梯形,AB∥CD,CD=3AB,过点B作平面PAD的平行线交直线PC于点E,则点PE:EC=1:2.