题目内容
其中第(1)(2)问文理科学生都要做,第(3)问按题目要求分文理来做。
已知 为坐标原点,向量
为坐标原点,向量 ,
,
 点
点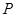 是直线
是直线 上的一点,且
上的一点,且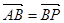 .
.
求点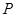 的坐标(用
的坐标(用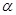 表示);
表示);
若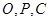 三点共线,求以线段
三点共线,求以线段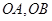 为邻边的平行四边形的对角线长;
为邻边的平行四边形的对角线长;
(3)(文科生做)记函数 •
•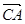 ,且
,且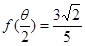 ,求
,求 的值.
的值.
(3)(理科生做)记函数 •
•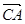 ,
,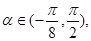 讨论函数
讨论函数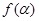 的单调性,并求其值域.
的单调性,并求其值域.
已知
 为坐标原点,向量
为坐标原点,向量 ,
,
 点
点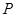 是直线
是直线 上的一点,且
上的一点,且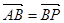 .
.求点
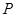 的坐标(用
的坐标(用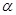 表示);
表示);若
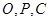 三点共线,求以线段
三点共线,求以线段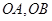 为邻边的平行四边形的对角线长;
为邻边的平行四边形的对角线长;(3)(文科生做)记函数
 •
•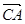 ,且
,且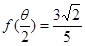 ,求
,求 的值.
的值.(3)(理科生做)记函数
 •
•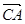 ,
,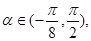 讨论函数
讨论函数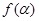 的单调性,并求其值域.
的单调性,并求其值域.(1)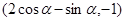 ;(2)
;(2)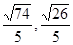 ;(3)(文)
;(3)(文)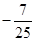 (理)
(理)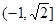 .
.
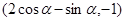 ;(2)
;(2)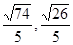 ;(3)(文)
;(3)(文)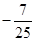 (理)
(理)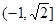 .
.试题分析:
解题思路:(1)利用向量的坐标运算和向量相等进行求解;(2)将三点共线转化为向量共线,再利用共线条件确定
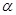 值,利用平行四边形法则与模长公式求解;(3)(文)先根据数量积公式得出
值,利用平行四边形法则与模长公式求解;(3)(文)先根据数量积公式得出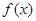 ,再求有关
,再求有关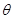 个三角函数值,再利用恒等变形求解;(理)先根据数量积公式得出
个三角函数值,再利用恒等变形求解;(理)先根据数量积公式得出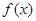 ,再利用
,再利用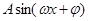 的图像与性质求解.
的图像与性质求解.规律总结:1.涉及平面向量运算问题,主要思路是:首先,利用平面向量基本定理,选择合适的向量作为基底,来表示有关向量;再利用数量积的有关公式进行求解(模长公式、夹角公式等);
2.涉及三角函数的最值或求值问题,往往先根据三角函数恒等变形化为
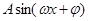 的形式,再利用三角函数的图像与性质进行求解.
的形式,再利用三角函数的图像与性质进行求解.试题解析:(1)设点
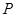 的坐标为
的坐标为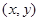 ,则
,则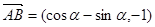 ,
,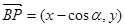
∵
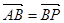 ,∴
,∴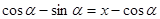 ,
,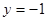
∴
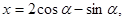
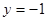
∴点
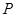 的坐标为
的坐标为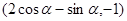
由
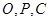 三点共线知:
三点共线知: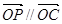 ,
,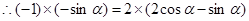 ,
,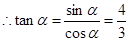
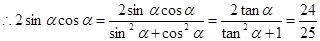
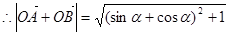 =
=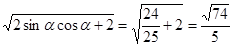
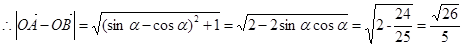
所以以
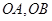 为邻边的平行四边形的对角线长分别为
为邻边的平行四边形的对角线长分别为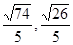
(3)(文科生做)∵
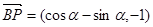 ,
,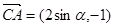
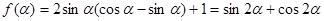 =
=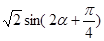
又
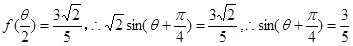
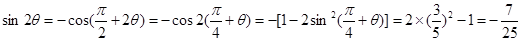
(3)(理科生做)∵
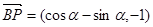 ,
,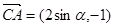
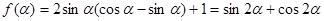 =
=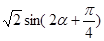
∵
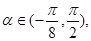 ∴
∴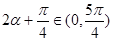 ,
, ∴
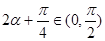 ,即
,即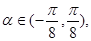 函数
函数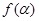 单调递增;
单调递增;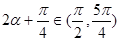 ,即
,即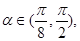 函数
函数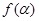 单调递减.
单调递减.且
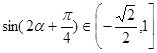 ,
,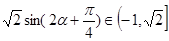
∴
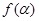 的值域为
的值域为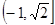 .
.
练习册系列答案
相关题目
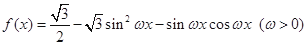 ,且
,且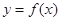 的图象的一个对称中心到最近的对称轴的距离为
的图象的一个对称中心到最近的对称轴的距离为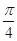 ,(1)求
,(1)求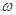 的值;(2)求
的值;(2)求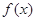 在区间
在区间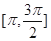 上的最大值和最小值.
上的最大值和最小值.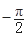 <j<0)图象上的任意两点,且角j的终边经过点P(l,-
<j<0)图象上的任意两点,且角j的终边经过点P(l,-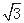 ),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为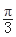 .
. 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.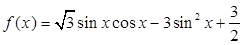 .
.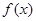 的最小正周期;
的最小正周期;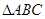 中,角
中,角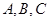 所对的边长分别为
所对的边长分别为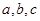 ,若
,若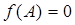 ,
,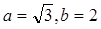 ,求
,求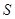 .
.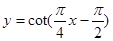 ,
,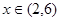
 的图象与
的图象与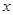 轴交于
轴交于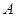 点,过点
点,过点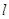 与函数的图象交于
与函数的图象交于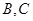 两点,则
两点,则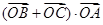
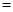 ( )
( )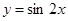 的图象向右平移
的图象向右平移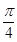 个单位,再向上平移1个单位,所得函数图象对应的解析式为( )
个单位,再向上平移1个单位,所得函数图象对应的解析式为( )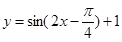



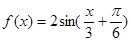 的图象向左平移
的图象向左平移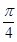 个单位,再向下平移
个单位,再向下平移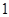 个单位,得到函数
个单位,得到函数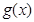 的图象,则
的图象,则



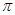 的偶函数是
的偶函数是 



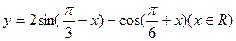 的最小值等于( )
的最小值等于( )